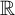 ${\mathbb R}$
${\mathbb R}$Published online by Cambridge University Press: 07 April 2022
Cantor’s first set theory paper (1874) establishes the uncountability of 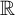 ${\mathbb R}$. We study this most basic mathematical fact formulated in the language of higher-order arithmetic. In particular, we investigate the logical and computational properties of
${\mathbb R}$. We study this most basic mathematical fact formulated in the language of higher-order arithmetic. In particular, we investigate the logical and computational properties of  ${\mathsf {NIN}}$ (resp.
${\mathsf {NIN}}$ (resp.  ${\mathsf {NBI}}$), i.e., the third-order statement there is no injection resp. bijection from
${\mathsf {NBI}}$), i.e., the third-order statement there is no injection resp. bijection from 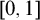 $[0,1]$ to
$[0,1]$ to 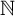 ${\mathbb N}$. Working in Kohlenbach’s higher-order Reverse Mathematics, we show that
${\mathbb N}$. Working in Kohlenbach’s higher-order Reverse Mathematics, we show that  ${\mathsf {NIN}}$ and
${\mathsf {NIN}}$ and  ${\mathsf {NBI}}$ are hard to prove in terms of (conventional) comprehension axioms, while many basic theorems, like Arzelà’s convergence theorem for the Riemann integral (1885), are shown to imply
${\mathsf {NBI}}$ are hard to prove in terms of (conventional) comprehension axioms, while many basic theorems, like Arzelà’s convergence theorem for the Riemann integral (1885), are shown to imply  ${\mathsf {NIN}}$ and/or
${\mathsf {NIN}}$ and/or  ${\mathsf {NBI}}$. Working in Kleene’s higher-order computability theory based on S1–S9, we show that the following fourth-order process based on
${\mathsf {NBI}}$. Working in Kleene’s higher-order computability theory based on S1–S9, we show that the following fourth-order process based on  ${\mathsf {NIN}}$ is similarly hard to compute: for a given
${\mathsf {NIN}}$ is similarly hard to compute: for a given 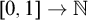 $[0,1]\rightarrow {\mathbb N}$-function, find reals in the unit interval that map to the same natural number.
$[0,1]\rightarrow {\mathbb N}$-function, find reals in the unit interval that map to the same natural number.