Article contents
On the ring of differentially-algebraic entire functions
Published online by Cambridge University Press: 12 March 2014
Extract
Let 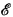 be the ring of all entire functions of one complex variable, and let DA be the subring of those entire functions that are differentially algebraic (DA); that is, they satisfy a nontrivial algebraic differential equation.
be the ring of all entire functions of one complex variable, and let DA be the subring of those entire functions that are differentially algebraic (DA); that is, they satisfy a nontrivial algebraic differential equation.
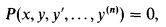
where P is a non-identically-zero polynomial in its n + 2 variables. It seems not to be known whether DA is elementarily equivalent to  . This would mean that DA and
. This would mean that DA and  have exactly the same true statements about them, in the first-order language of rings. (Roughly speaking, a sentence about a ring R is first-order if it has finite length and quantifies only over elements (i.e., not subsets or functions or relations) of R.) It follows from [NAN] that DA and
have exactly the same true statements about them, in the first-order language of rings. (Roughly speaking, a sentence about a ring R is first-order if it has finite length and quantifies only over elements (i.e., not subsets or functions or relations) of R.) It follows from [NAN] that DA and 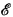 are not isomorphic as rings, but this does not answer the question of elementary equivalence.
are not isomorphic as rings, but this does not answer the question of elementary equivalence.
Information
- Type
- Research Article
- Information
- Copyright
- Copyright © Association for Symbolic Logic 1992
References
REFERENCES
- 2
- Cited by

