No CrossRef data available.
Article contents
On the independence of Henkin's axioms for fragments of the propositional calculus
Published online by Cambridge University Press: 12 March 2014
Extract
A general system of axioms has been given by Henkin for a fragment of the propositional calculus having as primitive symbols, in addition to the usual parentheses, variables, and implication sign ⊃, an arbitrarily given truth function symbol ϕ. This system of axioms, which we shall denote by S(⊃, ϕ), contains the following three axiom schemata
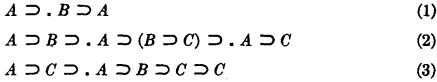
plus the 2m further axiom schemata involving the symbol ϕ
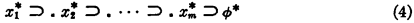
where ϕ is an m-placed function symbol. We refer to Henkin's paper, p. 43, for the detailed description of the axiom schemata (4).
The remark was made in the above mentioned paper that each of the 2m axiom schemata of (4) is trivially independent of the rest of the axioms of S(⊃, ϕ), and it was conjectured that the axiom schemata (1), (2) and (3) are also independent. In this note, we prove the general independence of the axiom schemata (1) and (2). As for (3), we show on the one hand its independence in the systems S(⊃) and S(⊃, f), and, on the other hand, its dependence in the system S(⊃, ∼). The net result is, therefore, that in any of these systems of axioms S(⊃, ϕ) all the axiom schemata are independent, except possibly the axiom schema (3).
Information
- Type
- Research Article
- Information
- Copyright
- Copyright © Association for Symbolic Logic 1951
References
1 See Henkin, Leon, Fragments of the propositional calculus, this Journal, vol. 14 (1949), pp. 42–48Google Scholar.

