Article contents
On the axiom of extensionality – Part I
Published online by Cambridge University Press: 12 March 2014
Extract
In part I of this paper it is shown that if the simple theory of types (with an axiom of infinity) is consistent, then so is the system obtained by adjoining axioms of extensionality; in part II a similar metatheorem for Gödel-Bernays set theory will be proved. The first of these results is of particular interest because type theory without the axioms of extensionality is fundamentally rather a simple system, and it should, I believe, be possible to prove that it is consistent.
Let us consider — in some unspecified formal system — a typical expression of the axiom of extensionality; for example:
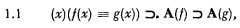
where A(h) is a formula, and A(f), A(g) are the results of substituting in it the predicate variagles f, g for the free variable h. Evidently, if the system considered contains the predicate calculus, and if h occurs in A(h) only in parts of the form h(t) where t is a term which lies within the range of the quantifier (x), then 1.1 will be provable. But this will not be so in general; indeed, by introducing into the system an intensional predicate of predicates we can make 1.1 false. For example, Myhill introduces a constant S, where ‘Sϕψχω’ means that (the expression) ϕ is the result of substituting ψ for χ in ω.
Information
- Type
- Research Article
- Information
- Copyright
- Copyright © Association for Symbolic Logic 1956
References
1 Indeed A. M. Turing once told me that he had done this, and that the proof was fairly difficult. I have found among his manuscripts two versions of the proof: one is rather short and contains a fallacy which could not, I think, easily be put right; the other (perhaps a second draft) is unfinished and only a beginning. He may therefore have discovered and surmounted the fallacy. On the other hand he always spoke of the axiom of extensionality as being ‘the nigger in the woodpile’, which suggests that he did not think his consistency proof was transcendental enough to accord with Gödel's theorem; but, by the results of this paper, it would have to be just that.
2 Myhill, J., The consistency of the axiom of reducibility, this Journal, vol. 16 (1951), pp. 35–42.Google Scholar
3 Frege refers to the axiom of extensionality as ‘a fundamental law of logic’, which he thinks is indemonstrable; see Funktion und Begriff translated in Translations from the philosophical writings of Gottlob Frege, Oxford, 1952, p. 26Google Scholar. For a proof of the independence of the axiom (in set theory), see Robinson, A., On the independence of the axioms of definiieness, this Journal, vol. 4 (1939), pp. 69–72.Google Scholar
4 In fact, of course, there is no need for such a relative consistency proof, as there exist consistency proofs for the whole system, axiom of extensionality included.
5 See e.g. Carnap, R., The logical syntax of language, London, 1937, p. 245Google Scholar.
6 See Church, Alonzo, A formulation of the simple theory of types, this Journal, vol. 5 (1940), pp. 56–68Google Scholar.
7 In Probleme der Grundlegung der Mathematik, Mathematische Annalen, vol. 102 (1929), pp. 1–9Google Scholar.
8 Proofs will be given in my forthcoming book The simple theory of types; the general line of attack is similar to that used in the present paper. A. M. Turing proved that (OCE) extends to (OCDE).
9 In The consistency of the axiom of choice and of the generalised continuum-hypothesis, Proceedings of the National Academy of Sciences, vol. 24 (1938), pp. 556–557CrossRefGoogle Scholar, Gödel states that his method is applicable to Tarski's formulation of the simple theory of types.
10 Some of these conventions were introduced by Newman, M. H. A. and Turing, A. M. in A formal theorem in Church's theory of types, this Journal, vol. 7 (1942), pp. 28–33Google Scholar.
11 Provided xα does not occur free in F oα.
12 This method of defining descriptions operators for the higher types is due to Church, op. cit., p. 62.
13 By induction on the type it is easy to show ![]() .
.
- 20
- Cited by

