Article contents
On simplifying truth-functional formulas
Published online by Cambridge University Press: 12 March 2014
Extract
The following are some consequences of a recent result concerning the prime implicants of disjunctive normal formulas.
I. Introduce the void fundamental formula λ, and define the consensus of αϕ and 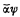 as in [5], but allowing ϕ or ψ or both to be λ. Then a normal formula Φ is valid if and only if the operations of dropping subsuming clauses and adjoining consensus formulas end by transforming Φ into the single formula λ. (For under the notions of fundamental formula and consensus as now extended, λ is a (unique) prime implicant of all valid formulas and of no others; and the argument of [5] now shows that the operations mentioned transform every normal formula, whether valid or not, into the disjunction of its prime implicants.)
as in [5], but allowing ϕ or ψ or both to be λ. Then a normal formula Φ is valid if and only if the operations of dropping subsuming clauses and adjoining consensus formulas end by transforming Φ into the single formula λ. (For under the notions of fundamental formula and consensus as now extended, λ is a (unique) prime implicant of all valid formulas and of no others; and the argument of [5] now shows that the operations mentioned transform every normal formula, whether valid or not, into the disjunction of its prime implicants.)
II. A normal formula ψ implies a normal formula Φ if and only if every clause of ψ subsumes one of the prime implicants of Φ, which are found as in I above. (The condition is clearly sufficient. It is necessary, for if ψ implies Φ, then every clause of ψ implies Φ and subsumes a shortest fundamental formula implying Φ.) In this condition, the prime implicants of Φ may be replaced by the clauses of the result of merely adjoining, as long as possible, consensus formulas to Φ.
Information
- Type
- Research Article
- Information
- Copyright
- Copyright © Association for Symbolic Logic 1956
References
REFERENCES
- 6
- Cited by

