Article contents
On sentences which are true of direct unions of algebras1
Published online by Cambridge University Press: 12 March 2014
Extract
It is well known that certain sentences corresponding to similar algebras are invariant under direct union; that is, are true of the direct union when true of each factor algebra. An axiomatizable class of similar algebras, such as the class of groups, is closed under direct union when each of its axioms is invariant. In this paper we shall determine a wide class of invariant sentences. We shall also be concerned with determining sentences which are true of a direct union provided they are true of some factor algebra. In the case where all the factor algebras are the same, a further result is obtained. In §2 it will be shown that these criteria are the only ones of their kind. Lemma 7 below may be of some independent interest.
We adopt the terminology and notation of McKinsey with the exception that the sign · will be used for conjunction. Expressions of the form ∼∊, where ∊ is an equation, will be called inequalities. In accordance with the analogy between conjunction and disjunction with product and sum respectively, we shall call α1, …, αn the terms of the disjunction
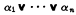
and the factors of the conjunction
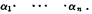
Every closed sentence is equivalent to a sentence in prenez normal form,
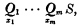
where x1, …, xm distinct individual variables, Q1, …, Qm are quantifiers, and the matrix S is an open sentence in which each of the variables x1, …, xm actually occurs. The sentence S may be written in either disjunctive normal form:
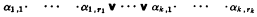
where αi,j is either an equation or an inequality, or in conjunctive normal form:
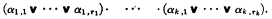 .
.
Information
- Type
- Research Article
- Information
- Copyright
- Copyright © Association for Symbolic Logic 1951
Footnotes
The problem considered in this paper was suggested to the author by Professor Alfred Tarski in his seminar of Spring 1947 at the University of California.
References
2 For the terminology see McKinsey, J. C. C., The decision problem for some classes of sentences without quantifiers, this Journal, vol. 8 (1943), pp. 61–76Google Scholar. By a, factor algebra of the direct union of algebras Γi, we mean one of the algebras Γi.
3 A special case of one of our theorems was obtained by McKinsey, loc. cit., p. 65.
4 We shall not attempt to use a rigorous notation in the informal metamathematical language. In particular, quotation marks are omitted in most cases.
5 We shall not use the word term in McKinsey's sense in this paper.
6 If Γ = (K, O 1, … ) is an algebra, we shall for convenience write “x is an element of Γ” when strictly speaking we should write “x is an element of K.”
7 The author is indebted to Robert L. Vaught for pointing out that the present formulation of Lemmas 3 and 4 simplifies the proofs of Theorems 1 and 3.
8 This example is due to Joseph L. Hodges, Jr.
9 See Hilbert, D. and Bernays, P., Grundlagen der Mathematik, Berlin 1934, vol. 1, p. 57Google Scholar. When ∼P is tautologous, the class of constituents of p which appear in N(P) is empty.
- 223
- Cited by

