Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by Crossref.
Hrušák, Michael
and
Zapletal, Jindřich
2008.
Forcing with quotients.
Archive for Mathematical Logic,
Vol. 47,
Issue. 7-8,
p.
719.

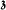 to be the smallest cardinality of a function
to be the smallest cardinality of a function 