Article contents
A note on the multiplicative semigroup of models of Peano arithmetic
Published online by Cambridge University Press: 12 March 2014
Extract
In a model 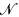 of Peano arithmetic, the isomorphism type of the multiplicative semigroup uniquely determines the isomorphism type of the additive semigroup. In fact, for any prime p of
of Peano arithmetic, the isomorphism type of the multiplicative semigroup uniquely determines the isomorphism type of the additive semigroup. In fact, for any prime p of 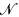 , the function x ↦ px is an isomorphism of the additive semigroup with the multiplicative subsemigroup of powers of p. It was observed by Jensen and Ehrenfeucht [3] that for countable models of PA, the isomorphism type of the additive semigroup (or even the additive group) determines the isomorphism type of the multiplicative semigroup. (See Theorem 3 below.)
, the function x ↦ px is an isomorphism of the additive semigroup with the multiplicative subsemigroup of powers of p. It was observed by Jensen and Ehrenfeucht [3] that for countable models of PA, the isomorphism type of the additive semigroup (or even the additive group) determines the isomorphism type of the multiplicative semigroup. (See Theorem 3 below.)
In this note we will show that the countability restriction cannot be dropped. First, we show (as Theorem 2) that for uncountable models of PA the isomorphism type of the additive group never determines the isomorphism type of the multiplicative semigroup. Our main result is Theorem 5 in which we show that the isomorphism type of the additive semigroup need not determine the isomorphism type of the multiplicative semigroup, thereby improving upon Harnik [2], where Theorem 5 is proved under the assumption of ♢. For completeness, a sketch of the proof of the Jensen-Ehrenfeucht result is included.
The history of this paper begins with Nadel's question, asked in 1981, whether the countability assumption can be eliminated in the Jensen-Ehrenfeucht theorem. Soon afterwards, Nadel obtained the strong counterexample of Theorem 2, which applied to the additive group rather than the additive semigroup. A result of Pabion [8] shows that such a strong result is not possible for the additive semigroup.
Information
- Type
- Research Article
- Information
- Copyright
- Copyright © Association for Symbolic Logic 1989
References
REFERENCES
- 2
- Cited by

