Published online by Cambridge University Press: 12 March 2014
In what follows, L is a recursive language. The structures to be considered are L-structures with universe named by constants from ω. A structure 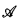 is recursive A if the open diagram D(
is recursive A if the open diagram D(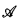 ) is recursive. Lerman and Schmerl [L-S] proved the following result.
) is recursive. Lerman and Schmerl [L-S] proved the following result.
Let T be an ℵ0-categorical elementary first-order theory. Suppose that for all n, 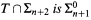 , and T is arithmetical. Then T has a recursive model.
, and T is arithmetical. Then T has a recursive model.
The aim of this paper is to extend Theorem 0.1. Stating the extension requires some terminology. Consider finitary formulas with symbols from L and sometimes extra constants from ω. For each n ∈ ω, the Σn and Πn formulas are as usual. Then Bnformulas are Boolean combinations of Σn formulas. For an L-structure 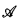 , Dn(
, Dn(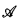 ) denotes the set of Bn sentences in the complete diagram Dc(
) denotes the set of Bn sentences in the complete diagram Dc(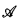 ). A complete Σn theory is a maximal consistent set of ΣnL-sentences. We may write φ(x), or Γ(x), to indicate that the free variables of the formula φ, or the set Γ, are among those in x. A complete Bn type for x is a maximal consistent set Γ(x) of Bn formulas with just the free variables x.
). A complete Σn theory is a maximal consistent set of ΣnL-sentences. We may write φ(x), or Γ(x), to indicate that the free variables of the formula φ, or the set Γ, are among those in x. A complete Bn type for x is a maximal consistent set Γ(x) of Bn formulas with just the free variables x.
If T is ℵ0-categorical, then for each x only finitely many complete types Γ(x) are consistent with T. While Lerman and Schmerl stated their result just for ℵ0-categorical theories, essentially the same proof yields the following.
Theorem 0.2. Let T be a consistent, complete theory such that for all n andx, only finitely many complete Bn types Γ(x) are consistent with T.