No CrossRef data available.
Published online by Cambridge University Press: 12 March 2014
We investigate the set S2 of “quickly sharped” reals:
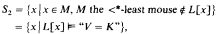
in the manner of [K] defining a natural hierarchy and quasi-hierarchy of constructibility degrees and identifying their termination points.