No CrossRef data available.
Article contents
MORE ON FRÉCHET–URYSOHN IDEALS
Published online by Cambridge University Press: 10 June 2021
Abstract
We study the Rudin–Keisler pre-order on Fréchet–Urysohn ideals on 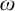 $\omega $. We solve three open questions posed by S. García-Ferreira and J. E. Rivera-Gómez in the articles [5] and [6] by establishing the following results:
$\omega $. We solve three open questions posed by S. García-Ferreira and J. E. Rivera-Gómez in the articles [5] and [6] by establishing the following results:
• For every AD family
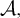 $\mathcal {A},$ there is an AD family
$\mathcal {A},$ there is an AD family 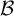 $\mathcal {B}$ such that
$\mathcal {B}$ such that 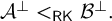 $\mathcal {A}^{\perp } <_{{\textsf {RK}}}\mathcal {B}^{\perp }.$
$\mathcal {A}^{\perp } <_{{\textsf {RK}}}\mathcal {B}^{\perp }.$• If
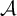 $\mathcal {A}$ is a nowhere MAD family of size
$\mathcal {A}$ is a nowhere MAD family of size 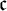 $\mathfrak {c}$ then there is a nowhere MAD family
$\mathfrak {c}$ then there is a nowhere MAD family 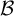 $\mathcal {B}$ such that
$\mathcal {B}$ such that 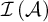 $\mathcal {I}\left (\mathcal {A}\right ) $ and
$\mathcal {I}\left (\mathcal {A}\right ) $ and 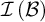 $\mathcal {I}\left ( \mathcal {B}\right ) $ are Rudin–Keisler incomparable.
$\mathcal {I}\left ( \mathcal {B}\right ) $ are Rudin–Keisler incomparable.• There is a family
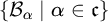 $\left \{ \mathcal {B}_{\alpha }\mid \alpha \in \mathfrak {c}\right \} $ of nowhere MAD families such that if
$\left \{ \mathcal {B}_{\alpha }\mid \alpha \in \mathfrak {c}\right \} $ of nowhere MAD families such that if 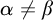 $\alpha \neq \beta $, then
$\alpha \neq \beta $, then 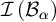 $\mathcal {I}\left ( \mathcal {B}_{\alpha }\right ) $ and
$\mathcal {I}\left ( \mathcal {B}_{\alpha }\right ) $ and 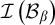 $\mathcal {I}\left ( \mathcal {B}_{\beta }\right ) $ are Rudin–Keisler incomparable.
$\mathcal {I}\left ( \mathcal {B}_{\beta }\right ) $ are Rudin–Keisler incomparable.
Here 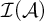 $\mathcal {I}(\mathcal {A})$ denotes the ideal generated by an AD family
$\mathcal {I}(\mathcal {A})$ denotes the ideal generated by an AD family  $\mathcal {A}$.
$\mathcal {A}$.
In the context of hyperspaces with the Vietoris topology, for a Fréchet–Urysohn-filter 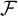 $\mathcal {F}$ we let
$\mathcal {F}$ we let  $\mathcal {S}_{c}\left ( \mathcal {\xi }\left ( \mathcal {F}\right ) \right ) $ be the hyperspace of nontrivial convergent sequences of the space consisting of
$\mathcal {S}_{c}\left ( \mathcal {\xi }\left ( \mathcal {F}\right ) \right ) $ be the hyperspace of nontrivial convergent sequences of the space consisting of 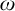 $\omega $ as discrete subset and only one accumulation point
$\omega $ as discrete subset and only one accumulation point 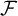 $\mathcal {F}$ whose neighborhoods are the elements of
$\mathcal {F}$ whose neighborhoods are the elements of 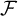 $\mathcal {F}$ together with the singleton
$\mathcal {F}$ together with the singleton 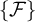 $\{\mathcal {F}\}$. For a FU-filter
$\{\mathcal {F}\}$. For a FU-filter 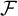 $\mathcal {F}$ we show that the following are equivalent:
$\mathcal {F}$ we show that the following are equivalent:
•
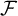 $\mathcal {F}$ is a FUF-filter.
$\mathcal {F}$ is a FUF-filter.•
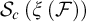 $\mathcal {S}_{c}\left ( \mathcal {\xi }\left ( \mathcal {F} \right ) \right ) $ is Baire.
$\mathcal {S}_{c}\left ( \mathcal {\xi }\left ( \mathcal {F} \right ) \right ) $ is Baire.
Information
- Type
- Article
- Information
- Copyright
- © The Author(s), 2021. Published by Cambridge University Press on behalf of The Association for Symbolic Logic


