Article contents
MODEL THEORY OF DERIVATIONS OF THE FROBENIUS MAP REVISITED
Published online by Cambridge University Press: 10 November 2021
Abstract
We prove some results about the model theory of fields with a derivation of the Frobenius map, especially that the model companion of this theory is axiomatizable by axioms used by Wood in the case of the theory 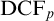 $\operatorname {DCF}_p$ and that it eliminates quantifiers after adding the inverse of the Frobenius map to the language. This strengthens the results from [4]. As a by-product, we get a new geometric axiomatization of this model companion. Along the way we also prove a quantifier elimination result, which holds in a much more general context and we suggest a way of giving “one-dimensional” axiomatizations for model companions of some theories of fields with operators.
$\operatorname {DCF}_p$ and that it eliminates quantifiers after adding the inverse of the Frobenius map to the language. This strengthens the results from [4]. As a by-product, we get a new geometric axiomatization of this model companion. Along the way we also prove a quantifier elimination result, which holds in a much more general context and we suggest a way of giving “one-dimensional” axiomatizations for model companions of some theories of fields with operators.
MSC classification
Information
- Type
- Article
- Information
- Copyright
- © The Author(s), 2021. Published by Cambridge University Press on behalf of The Association for Symbolic Logic
References
- 3
- Cited by


