Article contents
Measurable chromatic numbers
Published online by Cambridge University Press: 12 March 2014
Abstract
We show that if add(null) = c, then the globally Baire and universally measurable chromatic numbers of the graph of any Borel function on a Polish space are equal and at most three. In particular, this holds for the graph of the unilateral shift on [ℕ]ℕ, although its Borel chromatic number is ℵ0. We also show that if add(null) = c, then the universally measurable chromatic number of every treeing of a measure amenable equivalence relation is at most three. In particular, this holds for “the” minimum analytic graph 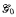 with uncountable Borel (and Baire measurable) chromatic number. In contrast, we show that for all κ Є6 (2, 3…..ℵ0, c), there is a treeing of E0 with Borel and Baire measurable chromatic number κ. Finally, we use a Glimm–Effros style dichotomy theorem to show that every basis for a non-empty initial segment of the class of graphs of Borel functions of Borel chromatic number at least three contains a copy of (ℝ<ℕ, ⊇).
with uncountable Borel (and Baire measurable) chromatic number. In contrast, we show that for all κ Є6 (2, 3…..ℵ0, c), there is a treeing of E0 with Borel and Baire measurable chromatic number κ. Finally, we use a Glimm–Effros style dichotomy theorem to show that every basis for a non-empty initial segment of the class of graphs of Borel functions of Borel chromatic number at least three contains a copy of (ℝ<ℕ, ⊇).
Information
- Type
- Research Article
- Information
- Copyright
- Copyright © Association for Symbolic Logic 2008
References
REFERENCES
- 4
- Cited by

