Article contents
Martin's axioms, measurability and equiconsistency results
Published online by Cambridge University Press: 12 March 2014
Abstract
We deal with the consistency strength of ZFC + variants of MA + suitable sets of reals are measurable (and/or Baire, and/or Ramsey). We improve the theorem of Harrington and Shelah [2] repairing the asymmetry between measure and category, obtaining also the same result for Ramsey. We then prove parallel theorems with weaker versions of Martin's axiom (MA(σ-centered), (MA(σ-linked)), 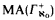 , MA(K)), getting Mahlo, inaccessible and weakly compact cardinals respectively. We prove that if there exists r ∈ R such that
, MA(K)), getting Mahlo, inaccessible and weakly compact cardinals respectively. We prove that if there exists r ∈ R such that 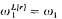 and MA holds, then there exists a
and MA holds, then there exists a  -selective filter on ω, and from the consistency of ZFC we build a model for ZFC + MA(I) + every
-selective filter on ω, and from the consistency of ZFC we build a model for ZFC + MA(I) + every  -set of reals is Lebesgue measurable, has the property of Baire and is Ramsey.
-set of reals is Lebesgue measurable, has the property of Baire and is Ramsey.
Information
- Type
- Research Article
- Information
- Copyright
- Copyright © Association for Symbolic Logic 1989
References
REFERENCES
- 13
- Cited by

