Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by Crossref.
Živaljević, Boško
1993.
Graphs with ∏ 1 0 (K)Y-sections.
Archive for Mathematical Logic,
Vol. 32,
Issue. 4,
p.
259.
Živaljević, Boško
1995.
Π¹₁ functions are almost internal.
Transactions of the American Mathematical Society,
Vol. 347,
Issue. 7,
p.
2621.
Render, Hermann
1995.
Countably determined sets and a conjecture of C.W. Henson.
Mathematische Annalen,
Vol. 303,
Issue. 1,
p.
307.
Zivaljevic, Bosko
1996.
Π₁¹ sets of unbounded Loeb measure.
Proceedings of the American Mathematical Society,
Vol. 124,
Issue. 7,
p.
2205.


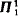 subset
subset 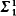 set is given.
set is given.