Published online by Cambridge University Press: 22 April 2015
The relativized weak pigeonhole principle states that if at least 2n out of n2 pigeons fly into n holes, then some hole must be doubly occupied. We prove that every DNF-refutation of the CNF encoding of this principle requires size 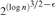 $2^{\left( {{\rm{log\ }}n} \right)^{3/2 - \varepsilon } } $ for every ε﹥0 and every sufficiently large n. By reducing it to the standard weak pigeonhole principle with 2n pigeons and n holes, we also show that this lower bound is essentially tight in that there exist DNF-refutations of size
$2^{\left( {{\rm{log\ }}n} \right)^{3/2 - \varepsilon } } $ for every ε﹥0 and every sufficiently large n. By reducing it to the standard weak pigeonhole principle with 2n pigeons and n holes, we also show that this lower bound is essentially tight in that there exist DNF-refutations of size 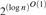 $2^{\left( {{\rm{log\ }}n} \right)^{O\left( 1 \right)} } $ even in R(log). For the lower bound proof we need to discuss the existence of unbalanced low-degree bipartite expanders satisfying a certain robustness condition.
$2^{\left( {{\rm{log\ }}n} \right)^{O\left( 1 \right)} } $ even in R(log). For the lower bound proof we need to discuss the existence of unbalanced low-degree bipartite expanders satisfying a certain robustness condition.