Article contents
Limit ultrapowers and abstract logics
Published online by Cambridge University Press: 12 March 2014
Abstract
We associate with any abstract logic L a family F(L) consisting, intuitively, of the limit ultrapowers which are complete extensions in the sense of L.
For every countably generated [ω, ω]-compact logic L, our main applications are:
(i) Elementary classes of L can be characterized in terms of ≡L only.
(ii) If 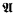 and
and 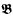 are countable models of a countable superstable theory without the finite cover property, then
are countable models of a countable superstable theory without the finite cover property, then 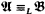 .
.
(iii) There exists the “largest” logic M such that complete extensions in the sense of M and L are the same; moreover M is still [ω, ω]-compact and satisfies an interpolation property stronger than unrelativized ⊿-closure.
(iv) If L = Lωω(Qx), then cf(ωx) > ω and λω < ωx, for all λ < ωx.
We also prove that no proper extension of Lωω generated by monadic quantifiers is compact. This strengthens a theorem of Makowsky and Shelah. We solve a problem of Makowsky concerning Lκλ-compact cardinals. We partially solve a problem of Makowsky and Shelah concerning the union of compact logics.
Information
- Type
- Research Article
- Information
- Copyright
- Copyright © Association for Symbolic Logic 1987
References
REFERENCES
- 6
- Cited by

