Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by Crossref.
Macpherson, Dugald
1993.
Finite and Infinite Combinatorics in Sets and Logic.
p.
249.
Macpherson, Dugald
2011.
A survey of homogeneous structures.
Discrete Mathematics,
Vol. 311,
Issue. 15,
p.
1599.
Macpherson, Dugald
and
Tent, Katrin
2011.
Simplicity of some automorphism groups.
Journal of Algebra,
Vol. 342,
Issue. 1,
p.
40.
Ghadernezhad, Z.
and
Tent, K.
2014.
New simple groups with a BN-pair.
Journal of Algebra,
Vol. 414,
Issue. ,
p.
72.
Evans, David M.
Ghadernezhad, Zaniar
and
Tent, Katrin
2016.
Simplicity of the automorphism groups of some Hrushovski constructions.
Annals of Pure and Applied Logic,
Vol. 167,
Issue. 1,
p.
22.
Calderoni, Filippo
Kwiatkowska, Aleksandra
and
Tent, Katrin
2021.
Simplicity of the automorphism groups of order and tournament expansions of homogeneous structures.
Journal of Algebra,
Vol. 580,
Issue. ,
p.
43.
Kaplan, Itay
Riahi, Binyamin
and
Rodríguez Fanlo, Arturo
2025.
Automorphisms of the Rado meet-tree.
Journal of Algebra,
Vol. 677,
Issue. ,
p.
13.

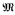 be a countable saturated structure, and assume that
be a countable saturated structure, and assume that 