Published online by Cambridge University Press: 12 March 2014
The theory of large cardinals in the absence of the axiom of choice (AC) has been examined extensively by set theorists. A particular motivation has been the study of large cardinals and their interrelationships with the axiom of determinacy (AD). Many important and beautiful theorems have been proven in this area, especially by Woodin, who has shown how to obtain, from hypermeasurability, models for the theories “ZF + DC + ∀α < ℵ1(ℵ1 → (ℵ1)α)” and 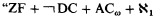
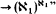 . Thus, consequences of AD whose consistency strength appeared to be beyond that of the more standard large cardinal hypotheses were shown to have suprisingly weak consistency strength.
. Thus, consequences of AD whose consistency strength appeared to be beyond that of the more standard large cardinal hypotheses were shown to have suprisingly weak consistency strength.
In this paper, we continue the study of large cardinals in the absence of AC and their interrelationships with AD by examining what large cardinal structures are possible on cardinals below ℵω in the absence of AC. Specifically, we prove the following theorems.
Theorem 1. Con(ZFC + κ1 < κ2are supercompact cardinals) ⇒ Con(ZF + DC + The club filter on ℵ1is a normal measure + ℵ1and ℵ2are supercompact cardinals).
Theorem 2. Con(ZF + AD) ⇒ Con(ZF + ℵ1, ℵ2and ℵ3are measurable cardinals which carry normal measures + μωis not a measure on any of these cardinals).