Published online by Cambridge University Press: 12 March 2014
In this paper we consider various properties of Jensen's □ principles and use them to construct several examples concerning the so-called Novák number of partially ordered sets.
In §1 we give the relevant definitions and review some facts about □ principles. Apart from some simple observations most of the results in this section are known.
In §2 we consider the Novák number of partially ordered sets and, using □ principles, give counterexamples to the productivity of this cardinal function. We also formulate a  principle, show by forcing that it is consistent and use it to construct an ℵ2-Suslin tree T such that forcing with T × T collapses ℵ1.
principle, show by forcing that it is consistent and use it to construct an ℵ2-Suslin tree T such that forcing with T × T collapses ℵ1.
In §3 we briefly consider games played on partially ordered sets and relate them to the problems of the previous section. Using a version of □ we give an example of a proper partial order 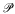 such that the game of length ω played on
such that the game of length ω played on 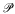 is undetermined.
is undetermined.
In §4 we raise the question of whether the Novák number of a homogenous partial order can be singular, and show that in some cases the answer is no.
We assume familiarity with the basic techniques of forcing. In §1 some facts about large cardinals (e.g. weakly compact cardinals are 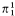 -indescribable) and elementary properties of the constructible hierarchy are used. For this and all undefined terms we refer the reader to Jech [10].
-indescribable) and elementary properties of the constructible hierarchy are used. For this and all undefined terms we refer the reader to Jech [10].