Article contents
Inverse topological systems and compactness in abstract model theory
Published online by Cambridge University Press: 12 March 2014
Abstract
Given an abstract logic 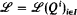 , generated by a set of quantifiers Qi, one can construct for each type τ a topological space Sτ, exactly as one constructs the Stone space for τ in first-order logic. Letting T be an arbitrary directed set of types, the set
, generated by a set of quantifiers Qi, one can construct for each type τ a topological space Sτ, exactly as one constructs the Stone space for τ in first-order logic. Letting T be an arbitrary directed set of types, the set 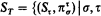
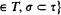 is an inverse topological system whose bonding mappings
is an inverse topological system whose bonding mappings 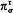 are naturally determined by the reduct operation on structures. We relate the compactness of
are naturally determined by the reduct operation on structures. We relate the compactness of 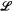 to the topological properties of ST. For example, if I is countable then
to the topological properties of ST. For example, if I is countable then  is compact iff for every τ each clopen subset of Sτ is of finite type and Sτ, is homeomorphic to limST, where T is the set of finite subtypes of τ. We finally apply our results to concrete logics.
is compact iff for every τ each clopen subset of Sτ is of finite type and Sτ, is homeomorphic to limST, where T is the set of finite subtypes of τ. We finally apply our results to concrete logics.
Information
- Type
- Research Article
- Information
- Copyright
- Copyright © Association for Symbolic Logic 1986
References
REFERENCES
[1]Barwise, K. J., Axioms for abstract model theory, Annals of Mathematical Logic, vol. 7 (1974), pp. 221–265.CrossRefGoogle Scholar
[2]Barwise, K. J. and Feferman, S. (editors), Model-theoretic logics, Springer-Verlag, New York, 1985.Google Scholar
[3]Barwise, K. J., Kaufmann, M. and Makkai, M., Stationary logic, Annals of Mathematical Logic, vol. 13 (1978), pp. 171–224.CrossRefGoogle Scholar
[6]Keisler, H. J., Logic with the quantifier “there exist uncountably many”, Annals of Mathematical Logic, vol. 1 (1970), pp. 1–93.CrossRefGoogle Scholar
[7]Lindström, P., On extensions of elementary logic, Theoria, vol. 35 (1969), pp. 1–11.CrossRefGoogle Scholar
[8]Magidor, M. and Malitz, J., Compact extensions of L(Q), Annals of Mathematical Logic, vol. 12 (1977), pp. 217–261.CrossRefGoogle Scholar
[9]Makowsky, J. A. and Mundici, D., Abstract equivalence relations, Chapter XIX in [2].Google Scholar
[10]Mundici, D., Applications of many-sorted Robinson consistency theorem, Zeitschrift für Mathematische Logik and Grundlagen der Mathematik, vol. 27 (1981), pp. 181–188.CrossRefGoogle Scholar
[11]Mundici, D., Duality between logics and equivalence relations, Transactions of the American Mathematical Society, vol. 270 (1982), pp. 111–129.CrossRefGoogle Scholar
[13]Shelah, S., Generalized quantifiers and compact logics, Transactions of the American Mathematical Society, vol. 204 (1975), pp. 342–364.CrossRefGoogle Scholar
[14]Mundici, D., Abstract model-theory and nets of C*-algebras: noncommutative interpolation and preservation properties, Models and sets (Proceedings of Logic Colloquium '83, Part 1), Lecture Notes in Mathematics, vol. 1103, Springer-Verlag, Berlin, 1984, pp. 351–377.Google Scholar
[15]Mundici, D., Mapping Abelian l-groups with strong unit one-one into MV algebras, Journal of Algebra, vol. 98 (1986), pp. 76–81.CrossRefGoogle Scholar
[16]Mundici, D., Interpolation of AF C*-algebras in Lukasiewicz sentential calculus, Journal of Functional Analysis, vol. 65 (1986), pp. 15–63.CrossRefGoogle Scholar
- 1
- Cited by

