No CrossRef data available.
Article contents
Injectives in finitely generated universal Horn classes
Published online by Cambridge University Press: 12 March 2014
Abstract
Let K be a finite set of finite structures. We give a syntactic characterization of the property: every element of K is injective in ISP(K). We use this result to establish that 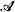 is injective in ISP(
is injective in ISP(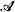 ) for every two-element algebra
) for every two-element algebra 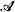 .
.
Information
- Type
- Research Article
- Information
- Copyright
- Copyright © Association for Symbolic Logic 1987
Footnotes
1
Research supported by an NSERC postdoctoral fellowship.
2
Research supported by an Ontario graduate scholarship.
References
REFERENCES
[1]
Albert, M. H., A preservation theorem for ec-structures with applications, this Journal, vol. 52 (1987), pp. 779–785.Google Scholar
[2]
Bacsich, P. D., Amalgamation properties and interpolation theorems for equational theories, Algebra Universalis, vol. 5 (1975), pp. 45–55.CrossRefGoogle Scholar
[3]
Balbes, R. and Dwinger, P., Distributive lattices, University of Missouri Press, Columbia, Missouri, 1974.Google Scholar
[4]
Bruns, G. and Lakser, H., Injective hulls of semilattices, Canadian Mathematical Bulletin, vol. 13 (1970), pp. 115–118.CrossRefGoogle Scholar
[5]
Burris, S. and Werner, H., Sheaf constructions and their elementary properties, Transactions of the American Mathematical Society, vol. 248 (1979), pp. 267–307.CrossRefGoogle Scholar
[7]
Lyndon, R. C., Identities in two-valued calculi, Transactions of the American Mathematical Society, vol. 71 (1951), pp. 457–465.CrossRefGoogle Scholar
[8]
Macintyre, A., Model completeness, Handbook of mathematical logic (Barwise, J., editor), North-Holland, Amsterdam, 1977, pp. 139–180.CrossRefGoogle Scholar
[9]
Post, E., Two-valued iterative systems of mathematical logic, Princeton University Press, Princeton, New Jersey, 1941.Google Scholar
[10]
Taylor, W., Pure compactifications in quasi-primal varieties, Canadian Journal of Mathematics, vol. 28 (1976), pp. 50–62.CrossRefGoogle Scholar

