Article contents
The independence of a weak axiom of choice1
Published online by Cambridge University Press: 12 March 2014
Extract
1. The purpose of this paper is to show that, if the axioms of a system G of set theory are consistent, then it is impossible to prove from them the following weak form of the axiom of choice: (H1) For every denumerable set x of disjoint two-element sets, there is a set y, called a choice set for x, which contains exactly one element in common with each element of x. Among the axioms of the system G, we take, with minor modifications, Axioms A, B, C of Gödel [6]. Clearly, the independence of H1 implies that of all stronger propositions, including the general axiom of choice and the generalized continuum hypothesis.
The proof depends upon ideas of Fraenkel and Mostowski, and proceeds in the following manner. Let a be a denumerable set of objects Δ0, Δ1, Δ2, …, the exact nature of which will be specified later. Let μj = {Δ2j, Δ2j+1} for each j, c = {μ0, μ1, μ2, …}, and b = [the sum set of a]. By transfinite induction, construct the class Vc which is the closure of b under the power-set operation. For each j, it is possible to define a 1–1 mapping 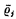 of Vc onto itself with the following properties. The mapping preserves the ε-relation, or, more precisely,
of Vc onto itself with the following properties. The mapping preserves the ε-relation, or, more precisely, 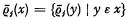 .
.
Information
- Type
- Research Article
- Information
- Copyright
- Copyright © Association for Symbolic Logic 1956
Footnotes
From a thesis in partial fulfillment of the requirements for the degree of Ph. D. in the Department of Mathematics of Cornell University, written while the author was a National Science Foundation Fellow in 1954–1955. The author would like to thank Professor J. Barkley Rosser for many helpful comments on the material of this paper.
References
BIBLIOGRAPHY
- 17
- Cited by

