Article contents
Honest bounds for complexity classes of recursive functions
Published online by Cambridge University Press: 12 March 2014
Extract
Let 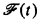 be the set of recursive functions computable by machines using at most t(x) computation steps on argument x, for all but finitely many inputs x. We call t a name for the complexity class
be the set of recursive functions computable by machines using at most t(x) computation steps on argument x, for all but finitely many inputs x. We call t a name for the complexity class 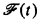 . Suppose we allow our machines to run longer, say h(x, t(x)) steps on argument x, where h is some fixed recursive function. One might expect that, for large enough h, permitting our machines to run longer by an amount h will always allow us to compute new functions, i.e.,
. Suppose we allow our machines to run longer, say h(x, t(x)) steps on argument x, where h is some fixed recursive function. One might expect that, for large enough h, permitting our machines to run longer by an amount h will always allow us to compute new functions, i.e., 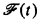 is a proper subset of
is a proper subset of 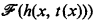 . This turns out not to be the case: The “gap theorem” ([2], [3]) implies that for every recursive h there exists a recursive t such that
. This turns out not to be the case: The “gap theorem” ([2], [3]) implies that for every recursive h there exists a recursive t such that 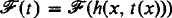 . However, if we restrict our attention to names from a certain subclass of the recursive functions, then we can indeed uniformly increase the size of our
. However, if we restrict our attention to names from a certain subclass of the recursive functions, then we can indeed uniformly increase the size of our 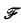 -classes. Informally, we call a recursive function t “honest” if some machine computes t(x) in roughly t(x) steps for each argument x. (A precise definition is given in Definition 1 below.) Then according to the “compression theorem” [1], there exists a single recursive function h such that, for every honest t,
-classes. Informally, we call a recursive function t “honest” if some machine computes t(x) in roughly t(x) steps for each argument x. (A precise definition is given in Definition 1 below.) Then according to the “compression theorem” [1], there exists a single recursive function h such that, for every honest t, 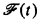 is a proper subset of
is a proper subset of 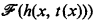 . Thus the phenomenon of the gap theorem is avoided by restricting attention to honest functions. It is a surprising consequence of the “honesty theorem” of McCreight and Meyer ([4], [5]) that there is no loss of generality in this restriction. Namely, for any recursive function t there is an honest recursive function t′ such that
. Thus the phenomenon of the gap theorem is avoided by restricting attention to honest functions. It is a surprising consequence of the “honesty theorem” of McCreight and Meyer ([4], [5]) that there is no loss of generality in this restriction. Namely, for any recursive function t there is an honest recursive function t′ such that 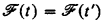 .
.
Information
- Type
- Research Article
- Information
- Copyright
- Copyright © Association for Symbolic Logic 1974
References
REFERENCES
- 4
- Cited by

