Article contents
HIGH DIMENSIONAL ELLENTUCK SPACES AND INITIAL CHAINS IN THE TUKEY STRUCTURE OF NON-P-POINTS
Published online by Cambridge University Press: 09 March 2016
Abstract
The generic ultrafilter 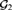 ${\cal G}_2 $ forced by
${\cal G}_2 $ forced by 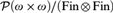 ${\cal P}\left( {\omega\times \omega } \right)/\left( {{\rm{Fin}} \otimes {\rm{Fin}}} \right)$ was recently proved to be neither maximum nor minimum in the Tukey order of ultrafilters ([1]), but it was left open where exactly in the Tukey order it lies. We prove
${\cal P}\left( {\omega\times \omega } \right)/\left( {{\rm{Fin}} \otimes {\rm{Fin}}} \right)$ was recently proved to be neither maximum nor minimum in the Tukey order of ultrafilters ([1]), but it was left open where exactly in the Tukey order it lies. We prove 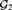 ${\cal G}_2 $ that is in fact Tukey minimal over its projected Ramsey ultrafilter. Furthermore, we prove that for each
${\cal G}_2 $ that is in fact Tukey minimal over its projected Ramsey ultrafilter. Furthermore, we prove that for each  ${\cal G}_2 $, the collection of all nonprincipal ultrafilters Tukey reducible to the generic ultrafilter
${\cal G}_2 $, the collection of all nonprincipal ultrafilters Tukey reducible to the generic ultrafilter 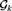 ${\cal G}_k $ forced by
${\cal G}_k $ forced by 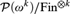 ${\cal P}\left( {\omega ^k } \right)/{\rm{Fin}}^{ \otimes k} $ forms a chain of length k. Essential to the proof is the extraction of a dense subset εk from (Fin⊗k)+ which we prove to be a topological Ramsey space. The spaces εk, k ≥ 2, form a hierarchy of high dimensional Ellentuck spaces. New Ramsey-classification theorems for equivalence relations on fronts on εk are proved, extending the Pudlák–Rödl Theorem for fronts on the Ellentuck space, which are applied to find the Tukey and Rudin–Keisler structures below
${\cal P}\left( {\omega ^k } \right)/{\rm{Fin}}^{ \otimes k} $ forms a chain of length k. Essential to the proof is the extraction of a dense subset εk from (Fin⊗k)+ which we prove to be a topological Ramsey space. The spaces εk, k ≥ 2, form a hierarchy of high dimensional Ellentuck spaces. New Ramsey-classification theorems for equivalence relations on fronts on εk are proved, extending the Pudlák–Rödl Theorem for fronts on the Ellentuck space, which are applied to find the Tukey and Rudin–Keisler structures below 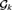 ${\cal G}_k $.
${\cal G}_k $.
Information
- Type
- Articles
- Information
- Copyright
- Copyright © The Association for Symbolic Logic 2016
References
REFERENCES
- 12
- Cited by

