Published online by Cambridge University Press: 19 June 2017
This paper considers a generalisation of selection functions over an arbitrary strong monad T, as functionals of type 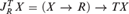 $J_R^T X = (X \to R) \to TX$ . It is assumed throughout that R is a T-algebra. We show that
$J_R^T X = (X \to R) \to TX$ . It is assumed throughout that R is a T-algebra. We show that 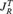 $J_R^T$ is also a strong monad, and that it embeds into the continuation monad
$J_R^T$ is also a strong monad, and that it embeds into the continuation monad 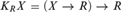 $K_R X = (X \to R) \to R$ . We use this to derive that the explicitly controlled product of T-selection functions is definable from the explicitly controlled product of quantifiers, and hence from Spector’s bar recursion. We then prove several properties of this product in the special case when T is the finite powerset monad
$K_R X = (X \to R) \to R$ . We use this to derive that the explicitly controlled product of T-selection functions is definable from the explicitly controlled product of quantifiers, and hence from Spector’s bar recursion. We then prove several properties of this product in the special case when T is the finite powerset monad 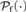 ${\cal P}_{\rm{f}} \left(\cdot\right)$ . These are used to show that when
${\cal P}_{\rm{f}} \left(\cdot\right)$ . These are used to show that when 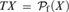 $TX = {\cal P}_{\rm{f}} \left( X \right)$ the explicitly controlled product of T-selection functions calculates a witness to the Herbrand functional interpretation of the double negation shift.
$TX = {\cal P}_{\rm{f}} \left( X \right)$ the explicitly controlled product of T-selection functions calculates a witness to the Herbrand functional interpretation of the double negation shift.