Article contents
The genericity conjecture
Published online by Cambridge University Press: 12 March 2014
Extract
The Genericity Conjecture, as stated in Beller-Jensen-Welch [1], is the following:
(*) If O # ∉ L[R], R ⊆ ω, then R is generic over L.
We must be precise about what is meant by “generic”.
Definition (Stated in Class Theory). A generic extension of an inner model M is an inner model M[G] such that for some forcing notion 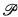 ⊆ M:
⊆ M:
(a) 〈M, 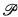 〉 is amenable and ⊩
〉 is amenable and ⊩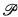 is 〈M,
is 〈M, 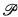 〉-definable for
〉-definable for 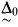 sentences.
sentences.
(b) G ⊆ 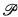 is compatible, closed upwards, and intersects every 〈M,
is compatible, closed upwards, and intersects every 〈M, 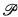 〉-definable dense D ⊆
〉-definable dense D ⊆ 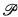 .
.
A set x is generic over M if it is an element of a generic extension of M. And x is strictly generic over M if M[x] is a generic extension of M.
Though the above definition quantifies over classes, in the special case where M = L and O # exists, these notions are in fact first order, as all L-amenable classes are 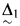 definable over L[O #]. From now on assume that O # exists.
definable over L[O #]. From now on assume that O # exists.
Theorem A. The Genericity Conjecture is false.
The proof is based upon the fact that every real generic over L obeys a certain definability property, expressed as follows.
Fact. If R is generic over L, then for some L-amenable class A, Sat〈L, A〉 is not definable over 〈L[R],A〉, where Sat〈L,A〉 is the canonical satisfaction predicate for 〈L,A〉.
Information
- Type
- Research Article
- Information
- Copyright
- Copyright © Association for Symbolic Logic 1994
References
REFERENCES
- 1
- Cited by

