Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by
Crossref.
Brendle, J.
1999.
Mutual Generics and Perfect Free Subsets.
Acta Mathematica Hungarica,
Vol. 82,
Issue. 1-2,
p.
143.
Spinas, Otmar
and
Thiele, Sonja
2010.
Additivity of the two-dimensional Miller ideal.
Archive for Mathematical Logic,
Vol. 49,
Issue. 6,
p.
617.
Laguzzi, Giorgio
2014.
On the separation of regularity properties of the reals.
Archive for Mathematical Logic,
Vol. 53,
Issue. 7-8,
p.
731.
Laguzzi, Giorgio
2014.
Some considerations on amoeba forcing notions.
Archive for Mathematical Logic,
Vol. 53,
Issue. 5-6,
p.
487.
Fischer, Vera
Friedman, Sy David
and
Khomskii, Yurii
2014.
Cichoń’s diagram, regularity properties and $${\varvec{\Delta}^1_3}$$ Δ 3 1 sets of reals.
Archive for Mathematical Logic,
Vol. 53,
Issue. 5-6,
p.
695.
Laguzzi, Giorgio
2015.
Generalized Silver and Miller measurability.
Mathematical Logic Quarterly,
Vol. 61,
Issue. 1-2,
p.
91.
Spinas, Otmar
2016.
Silver trees and Cohen reals.
Israel Journal of Mathematics,
Vol. 211,
Issue. 1,
p.
473.
Jossen, Sven
and
Spinas, Otmar
2017.
Logic Colloquium 2000.
p.
294.
Brendle, Jörg
2017.
Logic Colloquium '98.
p.
109.
Spinas, Otmar
2018.
No Tukey reduction of Lebesgue null to Silver null sets.
Journal of Mathematical Logic,
Vol. 18,
Issue. 02,
p.
1850011.
LAGUZZI, GIORGIO
2019.
UNCOUNTABLE TREES AND COHEN $\kappa$-REALS.
The Journal of Symbolic Logic,
Vol. 84,
Issue. 3,
p.
877.
Hein, Paul
and
Spinas, Otmar
2020.
Antichains of perfect and splitting trees.
Archive for Mathematical Logic,
Vol. 59,
Issue. 3-4,
p.
367.
Laguzzi, Giorgio
and
Stuber‐Rousselle, Brendan
2020.
More on trees and Cohen reals.
Mathematical Logic Quarterly,
Vol. 66,
Issue. 2,
p.
173.
Laguzzi, Giorgio
Mildenberger, Heike
and
Stuber‐Rousselle, Brendan
2023.
On splitting trees.
Mathematical Logic Quarterly,
Vol. 69,
Issue. 1,
p.
15.
Shelah, Saharon
and
Spinas, Otmar
2023.
Different cofinalities of tree ideals.
Annals of Pure and Applied Logic,
Vol. 174,
Issue. 8,
p.
103290.
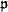 < add(m0), where add denotes the additivity coefficient of an ideal. For this we construct amoeba forcings for these forcings which do not add Cohen reals. We show that
< add(m0), where add denotes the additivity coefficient of an ideal. For this we construct amoeba forcings for these forcings which do not add Cohen reals. We show that 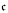 = ω2 implies add(m0) ≤
= ω2 implies add(m0) ≤ 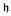 . We show that
. We show that 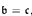 ,
, 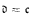 implies cov(ℓ0) ≤
implies cov(ℓ0) ≤ 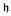 +, cov(m0) ≤
+, cov(m0) ≤ 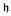 + respectively. Here cov denotes the covering coefficient. We also show that in the Cohen model cov(m0) <
+ respectively. Here cov denotes the covering coefficient. We also show that in the Cohen model cov(m0) < 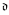 holds. Finally we prove that Cohen forcing does not add a superperfect tree of Cohen reals.
holds. Finally we prove that Cohen forcing does not add a superperfect tree of Cohen reals.
