Article contents
Generalizing special Aronszajn trees
Published online by Cambridge University Press: 12 March 2014
Extract
In this paper we define by means of a partition property a decreasing sequence N = ‹N α : α is an ordinal› of classes of ordinals. This property is a generalization of the nonexistence of special Aronszajn trees: the successor cardinal κ + is in N 0 iff there does not exist a special Aronszajn κ +-tree.
The interest in the classes N α stems from their applicability in model theory, in particular to that aspect of model theory dealing with ordered and two-cardinal models. A model 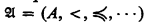 is κ-like iff < is a linear ordering of A of cardinality κ but such that every proper initial segment has cardinality < κ.
is κ-like iff < is a linear ordering of A of cardinality κ but such that every proper initial segment has cardinality < κ. 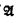 is α-ordered iff ≼ is a reflexive, linear ordering of some subset of A with order type α. The sequence N can be characterized by a first-order sentence σ in the following manner: The sentence σ has a κ-like α-ordered model iff κ ∉ Nα . This characterization will allow us to translate various independence statements regarding the sequence N to statements about the independence of transfer properties. We say that the transfer property κ → λ holds iff every first-order sentence which has a κ-like model also has a λ-like model. κ ⇸ λ is the negation of κ → λ.
is α-ordered iff ≼ is a reflexive, linear ordering of some subset of A with order type α. The sequence N can be characterized by a first-order sentence σ in the following manner: The sentence σ has a κ-like α-ordered model iff κ ∉ Nα . This characterization will allow us to translate various independence statements regarding the sequence N to statements about the independence of transfer properties. We say that the transfer property κ → λ holds iff every first-order sentence which has a κ-like model also has a λ-like model. κ ⇸ λ is the negation of κ → λ.
Information
- Type
- Research Article
- Information
- Copyright
- Copyright © Association for Symbolic Logic 1974
References
REFERENCES
- 4
- Cited by

