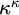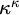1. Introduction
Definition 1. Let
![]() $\kappa \leq \lambda $
be regular cardinals. We call a sequence
$\kappa \leq \lambda $
be regular cardinals. We call a sequence
![]() $\langle a_\xi : \xi \in \lambda \rangle $
, where
$\langle a_\xi : \xi \in \lambda \rangle $
, where
![]() $a_\xi $
is a subset of
$a_\xi $
is a subset of
![]() $\kappa $
of cardinality
$\kappa $
of cardinality
![]() $\kappa $
, i.e.,
$\kappa $
, i.e.,
![]() $a_\xi \in [\kappa ]^{\kappa }$
, a
$a_\xi \in [\kappa ]^{\kappa }$
, a
![]() $\kappa $
-tower of length
$\kappa $
-tower of length
![]() $\lambda $
iff
$\lambda $
iff
-
(i) For all
 $\xi < \xi ' < \lambda : a_\xi \supseteq ^{*} a_{\xi '}$
, i.e.,
$\xi < \xi ' < \lambda : a_\xi \supseteq ^{*} a_{\xi '}$
, i.e.,
 $|a_{\xi '} \setminus a_{\xi }|< \kappa $
,
$|a_{\xi '} \setminus a_{\xi }|< \kappa $
, -
(ii) There does not exist an
 $a \in [\kappa ]^{\kappa }$
with
$a \in [\kappa ]^{\kappa }$
with
 $\forall \xi < \lambda : a_\xi \supseteq ^{*}a$
(no pseudo-intersection).
$\forall \xi < \lambda : a_\xi \supseteq ^{*}a$
(no pseudo-intersection).
Let
![]() $\mathfrak {sp}(\mathfrak {t}(\kappa )):=\{\lambda : \text {there exists a }\kappa \text {-tower of length }\lambda \}$
be the
$\mathfrak {sp}(\mathfrak {t}(\kappa )):=\{\lambda : \text {there exists a }\kappa \text {-tower of length }\lambda \}$
be the
![]() $\kappa $
-tower spectrum and
$\kappa $
-tower spectrum and
![]() $\mathfrak {t}(\kappa ):=\min (\mathfrak {sp}(\mathfrak {t}(\kappa )))$
the
$\mathfrak {t}(\kappa ):=\min (\mathfrak {sp}(\mathfrak {t}(\kappa )))$
the
![]() $\kappa $
-tower number.
$\kappa $
-tower number.
Note that this definition excludes towers of non-regular length and of length
![]() ${<}\kappa $
, i.e.,
${<}\kappa $
, i.e.,
![]() $\mathfrak {sp}(\mathfrak {t}(\kappa ))$
is a set of regular cardinals above
$\mathfrak {sp}(\mathfrak {t}(\kappa ))$
is a set of regular cardinals above
![]() $\kappa $
. This is of course no real restriction, since we can always extract a cofinal subsequence from any ordinal-length tower. Conversely, we can always artificially extend a tower as in the definition to an ordinal-length tower by repeating elements. The requirement that
$\kappa $
. This is of course no real restriction, since we can always extract a cofinal subsequence from any ordinal-length tower. Conversely, we can always artificially extend a tower as in the definition to an ordinal-length tower by repeating elements. The requirement that
![]() $\lambda \geq \kappa $
is a consequence of the following pathology that arises in the generalized Baire spaces:
$\lambda \geq \kappa $
is a consequence of the following pathology that arises in the generalized Baire spaces:
Fact 1. Let
![]() $\kappa $
be regular and uncountable. Decompose
$\kappa $
be regular and uncountable. Decompose
![]() $\kappa $
as
$\kappa $
as
![]() $\kappa :=\bigcup _{n\in \omega }X_n$
, where each
$\kappa :=\bigcup _{n\in \omega }X_n$
, where each
![]() $X_n$
has cardinality
$X_n$
has cardinality
![]() $\kappa $
. Then the family
$\kappa $
. Then the family
![]() $\{\bigcup _{m \geq n} X_m: n \in \omega \}$
is well-ordered by
$\{\bigcup _{m \geq n} X_m: n \in \omega \}$
is well-ordered by
![]() $\supseteq ^{*}$
and has no pseudo-intersection.
$\supseteq ^{*}$
and has no pseudo-intersection.
The
![]() $\omega $
-tower spectrum has been well-studied for many decades, for example by Hechler in [Reference Hechler7], by Baumgartner and Dordal in [Reference Baumgartner and Dordal2] or by Dordal in [Reference Dordal4]. In particular, Hechler [Reference Hechler7] showed that consistently, there exists an
$\omega $
-tower spectrum has been well-studied for many decades, for example by Hechler in [Reference Hechler7], by Baumgartner and Dordal in [Reference Baumgartner and Dordal2] or by Dordal in [Reference Dordal4]. In particular, Hechler [Reference Hechler7] showed that consistently, there exists an
![]() $\omega $
-tower of length
$\omega $
-tower of length
![]() $\lambda $
for each regular
$\lambda $
for each regular
![]() $\lambda \in [\omega _1,\,2^\omega ]$
. Dordal [Reference Dordal4, Corollary 2.6] showed that for any set A of regular cardinals containing all of its regular limit points and the successors of its singular limit points (A is an Easton set), it is consistent that
$\lambda \in [\omega _1,\,2^\omega ]$
. Dordal [Reference Dordal4, Corollary 2.6] showed that for any set A of regular cardinals containing all of its regular limit points and the successors of its singular limit points (A is an Easton set), it is consistent that
![]() $\mathfrak {sp}(\mathfrak {t}(\omega ))=A$
.
$\mathfrak {sp}(\mathfrak {t}(\omega ))=A$
.
The present paper is motivated by the more recent interest in studying generalizations of classical cardinal invariants to the generalized Baire space
![]() $\kappa ^\kappa $
. In particular, we are interested in controlling invariants globally, i.e., for all regular
$\kappa ^\kappa $
. In particular, we are interested in controlling invariants globally, i.e., for all regular
![]() $\kappa $
simultaneously. This line of inquiry specifically can be seen as building upon Easton’s famous Theorem [Reference Easton5], which establishes global control over the class function
$\kappa $
simultaneously. This line of inquiry specifically can be seen as building upon Easton’s famous Theorem [Reference Easton5], which establishes global control over the class function
![]() $\kappa \to 2^\kappa $
. In particular, we follow recent work by Bağ, the first author and Friedman [Reference Bağ, Fischer and Friedman1], who analysed the spectrum of the generalized maximal almost-disjointness number globally.
$\kappa \to 2^\kappa $
. In particular, we follow recent work by Bağ, the first author and Friedman [Reference Bağ, Fischer and Friedman1], who analysed the spectrum of the generalized maximal almost-disjointness number globally.
In addition to
![]() $\mathfrak {t}(\kappa )$
, we need the following generalized cardinal invariants:
$\mathfrak {t}(\kappa )$
, we need the following generalized cardinal invariants:
Definition 2. Let
![]() $\kappa $
be a regular cardinal.
$\kappa $
be a regular cardinal.
-
(i) A subset
 $\mathcal {B}\subseteq \kappa ^\kappa $
is unbounded iff
$\mathcal {B}\subseteq \kappa ^\kappa $
is unbounded iff
 $\forall f \in \kappa ^\kappa \;\exists g \in \mathcal {B}: g \nleq ^{*}f$
, where
$\forall f \in \kappa ^\kappa \;\exists g \in \mathcal {B}: g \nleq ^{*}f$
, where
 $g \leq ^{*} f :\iff |\{\eta \in \kappa : g(\eta )>f(\eta )\}|< \kappa $
. Let
$g \leq ^{*} f :\iff |\{\eta \in \kappa : g(\eta )>f(\eta )\}|< \kappa $
. Let
 $\mathfrak {b}(\kappa ):=\min \{|\mathcal {B}|: \mathcal {B} \subseteq \kappa ^\kappa \;\text {is unbounded}\}$
be the
$\mathfrak {b}(\kappa ):=\min \{|\mathcal {B}|: \mathcal {B} \subseteq \kappa ^\kappa \;\text {is unbounded}\}$
be the
 $\kappa $
-bounding number.
$\kappa $
-bounding number. -
(ii) A subset
 $\mathcal {D}\subseteq \kappa ^\kappa $
is dominating iff
$\mathcal {D}\subseteq \kappa ^\kappa $
is dominating iff
 $\forall f\in \kappa ^\kappa \;\exists g \in \mathcal {D}: f \leq ^{*}g$
. Let
$\forall f\in \kappa ^\kappa \;\exists g \in \mathcal {D}: f \leq ^{*}g$
. Let
 $\mathfrak {d}(\kappa ):=\min \{|\mathcal {D}|: \mathcal {D} \subseteq \kappa ^\kappa \;\text {is dominating}\}$
be the
$\mathfrak {d}(\kappa ):=\min \{|\mathcal {D}|: \mathcal {D} \subseteq \kappa ^\kappa \;\text {is dominating}\}$
be the
 $\kappa $
-dominating number.
$\kappa $
-dominating number. -
(iii) A family
 $\mathcal {A} \subseteq [\kappa ]^\kappa $
is almost disjoint iff
$\mathcal {A} \subseteq [\kappa ]^\kappa $
is almost disjoint iff
 $\forall a \neq b \in \mathcal {A}: |a \cap b|< \kappa $
. Furthermore,
$\forall a \neq b \in \mathcal {A}: |a \cap b|< \kappa $
. Furthermore,
 $\mathcal {A}$
is maximal almost disjoint (
$\mathcal {A}$
is maximal almost disjoint (
 $\kappa $
-mad) if
$\kappa $
-mad) if
 $\mathcal {A}$
is not properly contained in a different almost disjoint family. Let
$\mathcal {A}$
is not properly contained in a different almost disjoint family. Let
 $\mathfrak {sp}(\mathfrak {a}(\kappa )):=\{\delta : \text {there exists a}\;\kappa \text {-mad family}\; \mathcal {A} \text { with } \kappa \leq |\mathcal {A}|=\delta \leq 2^\kappa \}$
be the
$\mathfrak {sp}(\mathfrak {a}(\kappa )):=\{\delta : \text {there exists a}\;\kappa \text {-mad family}\; \mathcal {A} \text { with } \kappa \leq |\mathcal {A}|=\delta \leq 2^\kappa \}$
be the
 $\kappa $
-mad spectrum and
$\kappa $
-mad spectrum and
 $\mathfrak {a}(\kappa ):=\min (\mathfrak {sp}(\mathfrak {a}(\kappa )))$
the
$\mathfrak {a}(\kappa ):=\min (\mathfrak {sp}(\mathfrak {a}(\kappa )))$
the
 $\kappa $
-maximal almost disjointness number.
$\kappa $
-maximal almost disjointness number. -
(iv) Let
 $\mathfrak {sp}(\mathfrak {t}_{\text {cl}}(\kappa )){\kern1pt}:={\kern1pt}\{\lambda : {\kern1pt}\text{there }{\kern1pt}\text{exists }{\kern1pt}\text{a }{\kern1pt}\kappa {\kern1pt}\text{-tower }{\kern1pt}\text{of }{\kern1pt}\text{length }{\kern1pt}\lambda {\kern1pt}\text{ consisting }{\kern1pt}\text{of }{\kern1pt}\text{club } \text{sets}\}$
and
$\mathfrak {sp}(\mathfrak {t}_{\text {cl}}(\kappa )){\kern1pt}:={\kern1pt}\{\lambda : {\kern1pt}\text{there }{\kern1pt}\text{exists }{\kern1pt}\text{a }{\kern1pt}\kappa {\kern1pt}\text{-tower }{\kern1pt}\text{of }{\kern1pt}\text{length }{\kern1pt}\lambda {\kern1pt}\text{ consisting }{\kern1pt}\text{of }{\kern1pt}\text{club } \text{sets}\}$
and
 $\mathfrak {t}_{\text {cl}}(\kappa ):=\min (\mathfrak {sp}(\mathfrak {t}_{\text {cl}}(\kappa )))$
.
$\mathfrak {t}_{\text {cl}}(\kappa ):=\min (\mathfrak {sp}(\mathfrak {t}_{\text {cl}}(\kappa )))$
.
The following basic fact, due to Schilhan [Reference Schilhan10], establishes that
![]() $\mathfrak {b}(\kappa )\in \mathfrak {sp}(\mathfrak {t}(\kappa ))$
for uncountable
$\mathfrak {b}(\kappa )\in \mathfrak {sp}(\mathfrak {t}(\kappa ))$
for uncountable
![]() $\kappa $
. It essentially follows by transforming
$\kappa $
. It essentially follows by transforming
![]() $f\in \kappa ^\kappa $
into the club
$f\in \kappa ^\kappa $
into the club
![]() $c_f:= \{\alpha \in \kappa : \forall \beta \in \alpha : f(\beta ) \in \alpha \}$
, and, vice versa, a club
$c_f:= \{\alpha \in \kappa : \forall \beta \in \alpha : f(\beta ) \in \alpha \}$
, and, vice versa, a club
![]() $c\in [\kappa ]^\kappa $
into the function
$c\in [\kappa ]^\kappa $
into the function
![]() $f_c(\alpha ):=\min (c\setminus (\alpha +1))$
.
$f_c(\alpha ):=\min (c\setminus (\alpha +1))$
.
Lemma 1 [Reference Schilhan10, Theorem 2.9]
Let
![]() $\kappa $
be regular uncountable. Then
$\kappa $
be regular uncountable. Then
![]() $\mathfrak {b}(\kappa )=\mathfrak {t}_{\text {cl}}(\kappa )$
.
$\mathfrak {b}(\kappa )=\mathfrak {t}_{\text {cl}}(\kappa )$
.
In the case
![]() $\kappa =\omega $
, we have the following:
$\kappa =\omega $
, we have the following:
Lemma 2 (Folklore)
Assume
![]() $\mathfrak {b}(\omega )< \mathfrak {d}(\omega )$
. Then
$\mathfrak {b}(\omega )< \mathfrak {d}(\omega )$
. Then
![]() $\mathfrak {b}(\omega ) \in \mathfrak {sp}(\mathfrak {t}(\omega ))$
.
$\mathfrak {b}(\omega ) \in \mathfrak {sp}(\mathfrak {t}(\omega ))$
.
Proof. Let
![]() $\mathcal {B} =\{g_\xi : \xi \in \mathfrak {b}(\omega )\}\subseteq \omega ^\omega $
be unbounded and such that
$\mathcal {B} =\{g_\xi : \xi \in \mathfrak {b}(\omega )\}\subseteq \omega ^\omega $
be unbounded and such that
![]() $\xi < \xi ' \implies g_\xi \leq ^{*} g_{\xi '}$
. Assume further that every
$\xi < \xi ' \implies g_\xi \leq ^{*} g_{\xi '}$
. Assume further that every
![]() $g_\xi \in \mathcal {B}$
is strictly increasing. Since
$g_\xi \in \mathcal {B}$
is strictly increasing. Since
![]() $\mathfrak {b}(\omega )< \mathfrak {d}(\omega )$
, there exists
$\mathfrak {b}(\omega )< \mathfrak {d}(\omega )$
, there exists
![]() $f\in \omega ^\omega $
that is not dominated by
$f\in \omega ^\omega $
that is not dominated by
![]() $\mathcal {B}$
. For each
$\mathcal {B}$
. For each
![]() $\xi \in \mathfrak {b}(\omega )$
, let
$\xi \in \mathfrak {b}(\omega )$
, let
![]() $a_\xi :=\{n \in \omega : f(n)> g_\xi (n)\}$
. Clearly, the sequence
$a_\xi :=\{n \in \omega : f(n)> g_\xi (n)\}$
. Clearly, the sequence
![]() $\langle a_\xi : \xi \in \mathfrak {b}(\omega )\rangle $
is well-ordered by
$\langle a_\xi : \xi \in \mathfrak {b}(\omega )\rangle $
is well-ordered by
![]() $\supseteq ^{*}$
. If it were pseudo-intersected by
$\supseteq ^{*}$
. If it were pseudo-intersected by
![]() $p \in [\omega ]^\omega $
, the function
$p \in [\omega ]^\omega $
, the function
![]() $f_p \in \omega ^\omega $
given by
$f_p \in \omega ^\omega $
given by
![]() $f_p(n):=f(\min (p\setminus (n+1)))$
would dominate
$f_p(n):=f(\min (p\setminus (n+1)))$
would dominate
![]() $\mathcal {B}$
.
$\mathcal {B}$
.
Note that if
![]() $\mathfrak {b}(\omega )=\mathfrak {d}(\omega )$
, the above conclusion consistently fails: After a
$\mathfrak {b}(\omega )=\mathfrak {d}(\omega )$
, the above conclusion consistently fails: After a
![]() $\lambda $
-stage finite-support iteration of Hechler forcing over a ground model satisfying
$\lambda $
-stage finite-support iteration of Hechler forcing over a ground model satisfying
![]() $\mathsf {CH}$
, we obtain a model in which
$\mathsf {CH}$
, we obtain a model in which
![]() $\mathfrak {b}(\omega )=\mathfrak {d}(\omega )=2^\omega =\lambda $
, but which contains no
$\mathfrak {b}(\omega )=\mathfrak {d}(\omega )=2^\omega =\lambda $
, but which contains no
![]() $\omega $
-towers of length
$\omega $
-towers of length
![]() $\lambda $
. This was shown by Baumgartner and Dordal [Reference Baumgartner and Dordal2, Theorem 4.1].
$\lambda $
. This was shown by Baumgartner and Dordal [Reference Baumgartner and Dordal2, Theorem 4.1].
The following well-known fact essentially follows from Lemma 1. For uncountable
![]() $\kappa $
, it is originally due to Shelah and Spasojević [Reference Shelah and Spasojević11].
$\kappa $
, it is originally due to Shelah and Spasojević [Reference Shelah and Spasojević11].
Fact 2 [Reference Shelah and Spasojević11, Fact 1.4]
For all regular
![]() $\kappa $
:
$\kappa $
:
![]() $\mathfrak {t}(\kappa ) \leq \mathfrak {b}(\kappa )$
.
$\mathfrak {t}(\kappa ) \leq \mathfrak {b}(\kappa )$
.
1.1. Structure of the paper
In Section 2, we begin by observing that in the Easton model, the
![]() $\kappa $
-tower spectrum is
$\kappa $
-tower spectrum is
![]() $\{\kappa ^{+}\}$
, globally. More specifically,
$\{\kappa ^{+}\}$
, globally. More specifically,
Theorem (Theorem 1)
For any Easton function E, it is consistent that
This will follow from a straightforward isomorphism-of-names argument. We then show that by a very similar argument, a small tower spectrum is consistent globally with an arbitrarily large
![]() $\kappa $
-mad spectrum:
$\kappa $
-mad spectrum:
Theorem (Theorem 2)
Let E be an index function such that for every
![]() $\kappa \in \text {dom}(E)$
,
$\kappa \in \text {dom}(E)$
,
![]() $E(\kappa )$
is a closed set of cardinals with
$E(\kappa )$
is a closed set of cardinals with
![]() $\min E(\kappa )\geq \kappa ^{+}$
,
$\min E(\kappa )\geq \kappa ^{+}$
,
![]() $\text {cf}(\max E(\kappa ))> \kappa $
and such that
$\text {cf}(\max E(\kappa ))> \kappa $
and such that
![]() $\kappa < \kappa ' \implies \max E(\kappa ) \leq \max E(\kappa ')$
. Then, consistently,
$\kappa < \kappa ' \implies \max E(\kappa ) \leq \max E(\kappa ')$
. Then, consistently,
Furthermore, by only controlling these spectra at successors of regular cardinals together with
![]() $\aleph _0$
, and restricting the range of E to so-called
$\aleph _0$
, and restricting the range of E to so-called
![]() $\kappa $
-Blass spectra, we have
$\kappa $
-Blass spectra, we have
Corollary (Corollary 1)
Let E be an index function defined on successors of regular cardinals together with
![]() $\aleph _0$
, and such that
$\aleph _0$
, and such that
![]() $E(\kappa )$
is a
$E(\kappa )$
is a
![]() $\kappa $
-Blass spectrum for every
$\kappa $
-Blass spectrum for every
![]() $\kappa \in \text {dom}(E)$
. Then, consistently,
$\kappa \in \text {dom}(E)$
. Then, consistently,
This is based on previous work by Bağ, the first author and Friedman [Reference Bağ, Fischer and Friedman1]. While the high-level argument is again an isomorphism of names, constructing the appropriate isomorphism turns out to be surprisingly convoluted. In Section 3, we show that arbitrarily large
![]() $\kappa $
-tower spectra are consistent globally. In fact, we show the following.
$\kappa $
-tower spectra are consistent globally. In fact, we show the following.
Theorem (Theorem 3 and Corollary 3)
Let E be an Easton function. Then, consistently,
Here,
![]() $[\kappa ^{+}, 2^\kappa ]$
denotes the set of regular cardinals between
$[\kappa ^{+}, 2^\kappa ]$
denotes the set of regular cardinals between
![]() $\kappa ^{+}$
and
$\kappa ^{+}$
and
![]() $2^\kappa $
. Finally, in Section 4, we prove that any non-trivial upper bound on the
$2^\kappa $
. Finally, in Section 4, we prove that any non-trivial upper bound on the
![]() $\kappa $
-tower spectrum is consistent. More precisely,
$\kappa $
-tower spectrum is consistent. More precisely,
Theorem (Theorem 4)
For any regular
![]() $\beta> \kappa $
and
$\beta> \kappa $
and
![]() $\mu $
with
$\mu $
with
![]() $\text {cf}(\mu )\geq \beta $
, it is consistent that
$\text {cf}(\mu )\geq \beta $
, it is consistent that
Tightness of this upper bound for uncountable
![]() $\kappa $
or for
$\kappa $
or for
![]() $\beta <\mu $
follows from Lemmas 1 and 2 above. Furthermore, Lemma 1 implies the following.
$\beta <\mu $
follows from Lemmas 1 and 2 above. Furthermore, Lemma 1 implies the following.
Corollary (Corollary 5)
For any regular uncountable
![]() $\kappa $
and
$\kappa $
and
![]() $\beta , \mu $
as above, it is consistent that
$\beta , \mu $
as above, it is consistent that
1.2. Convention
We say that a forcing notion
![]() $\mathbb {P}$
is
$\mathbb {P}$
is
![]() $\kappa $
-closed if every decreasing sequence of
$\kappa $
-closed if every decreasing sequence of
![]() $\mathbb {P}$
-conditions of length
$\mathbb {P}$
-conditions of length
![]() $\lambda < \kappa $
has a lower bound. Furthermore, we say that
$\lambda < \kappa $
has a lower bound. Furthermore, we say that
![]() $\mathbb {P}$
satisfies the
$\mathbb {P}$
satisfies the
![]() $\kappa $
-chain condition (
$\kappa $
-chain condition (
![]() $\kappa $
-c.c.) if antichains have size
$\kappa $
-c.c.) if antichains have size
![]() ${<}\kappa $
. For cardinals
${<}\kappa $
. For cardinals
![]() $\delta $
and
$\delta $
and
![]() $\gamma $
, we denote by
$\gamma $
, we denote by
![]() $[\delta , \gamma ]$
the set of regular cardinals between
$[\delta , \gamma ]$
the set of regular cardinals between
![]() $\delta $
and
$\delta $
and
![]() $\gamma $
.
$\gamma $
.
2. Globally small tower spectra
It is folklore that there are no towers of length
![]() ${>}\omega _1$
in the Cohen Model. We observe that this can be generalized to a global result.
${>}\omega _1$
in the Cohen Model. We observe that this can be generalized to a global result.
Definition 3.
-
(i) A function E is an index function if
 $\text {dom}(E)$
is a class of regular cardinals.
$\text {dom}(E)$
is a class of regular cardinals. -
(ii) An index function E is an Easton function if for every
 $\kappa \in \text {dom}(E)$
,
$\kappa \in \text {dom}(E)$
,
 $ E(\kappa )$
is a cardinal with
$ E(\kappa )$
is a cardinal with
 $\text {cf}(E(\kappa ))>\kappa $
and such that
$\text {cf}(E(\kappa ))>\kappa $
and such that
 $\kappa < \kappa ' \implies E(\kappa ) \leq E(\kappa ')$
.
$\kappa < \kappa ' \implies E(\kappa ) \leq E(\kappa ')$
.
If E is an index function and
![]() $\kappa \in \text {dom}(E)$
, we let
$\kappa \in \text {dom}(E)$
, we let
![]() $E^{\leq \kappa }:=E|_{\kappa +1}$
and
$E^{\leq \kappa }:=E|_{\kappa +1}$
and
![]() $E^{{>}\kappa }:=E|_{\text {dom}(E)\setminus (\kappa +1)}$
. Furthermore, if there is a forcing notion
$E^{{>}\kappa }:=E|_{\text {dom}(E)\setminus (\kappa +1)}$
. Furthermore, if there is a forcing notion
![]() $\mathbb {P}_\kappa $
for each
$\mathbb {P}_\kappa $
for each
![]() $\kappa \in \text {dom}(E)$
, the Easton-product
$\kappa \in \text {dom}(E)$
, the Easton-product
![]() $\mathbb {P}(E)$
of the
$\mathbb {P}(E)$
of the
![]() $\mathbb {P}_\kappa $
consists of conditions of the form
$\mathbb {P}_\kappa $
consists of conditions of the form
![]() $p=\langle p(\kappa ): \kappa \in \text {dom}(E)\rangle $
, where for each regular cardinal
$p=\langle p(\kappa ): \kappa \in \text {dom}(E)\rangle $
, where for each regular cardinal ![]() . The set
. The set ![]() is called the support of p and denoted by
is called the support of p and denoted by
![]() $\text {supp}(p)$
. It is clear that
$\text {supp}(p)$
. It is clear that
![]() $\mathbb {P}(E)$
is isomorphic to
$\mathbb {P}(E)$
is isomorphic to
![]() $\mathbb {P}(E^{\leq \kappa })\times \mathbb {P}(E^{>\kappa })$
.
$\mathbb {P}(E^{\leq \kappa })\times \mathbb {P}(E^{>\kappa })$
.
Definition 4. Let E be an Easton function. Easton forcing relative to E is the Easton-product of the forcing notions
![]() $\text {Fn}_{<\kappa }(E(\kappa ) \times \kappa , 2)$
over all
$\text {Fn}_{<\kappa }(E(\kappa ) \times \kappa , 2)$
over all
![]() $\kappa \in \text {dom}(E)$
.
$\kappa \in \text {dom}(E)$
.
It is well-known that for each
![]() $\kappa \in \text {dom}(E): \mathbb {P}(E^{\leq \kappa })$
satisfies the
$\kappa \in \text {dom}(E): \mathbb {P}(E^{\leq \kappa })$
satisfies the
![]() $\kappa ^{+}$
-c.c. and
$\kappa ^{+}$
-c.c. and
![]() $\mathbb {P}(E^{{>} \kappa })$
is
$\mathbb {P}(E^{{>} \kappa })$
is
![]() $\kappa ^{+}$
-closed, provided that
$\kappa ^{+}$
-closed, provided that
![]() $2^{<\kappa }=\kappa $
.
$2^{<\kappa }=\kappa $
.
Theorem 1. Let
![]() $\mathbf {V}\models \mathsf {GCH}$
, let E be an Easton function and denote Easton forcing relative to E by
$\mathbf {V}\models \mathsf {GCH}$
, let E be an Easton function and denote Easton forcing relative to E by
![]() $\mathbb {P}(E)$
. Then, in any
$\mathbb {P}(E)$
. Then, in any
![]() $\mathbb {P}(E)$
-generic extension of
$\mathbb {P}(E)$
-generic extension of
![]() $\mathbf {V}$
:
$\mathbf {V}$
:
Proof. The second equality is well-known. Fix
![]() $\kappa \in \text {dom}(E)$
and let G be
$\kappa \in \text {dom}(E)$
and let G be
![]() $\mathbb {P}({E})$
generic over
$\mathbb {P}({E})$
generic over
![]() $\mathbf {V}$
. Assume by contradiction that there exists a
$\mathbf {V}$
. Assume by contradiction that there exists a
![]() $\kappa $
-tower
$\kappa $
-tower
![]() $\langle a_\xi : \xi \in \lambda \rangle $
of length
$\langle a_\xi : \xi \in \lambda \rangle $
of length
![]() $\lambda \geq \kappa ^{++}$
in
$\lambda \geq \kappa ^{++}$
in
![]() $\mathbf {V}[G]$
. We can assume that
$\mathbf {V}[G]$
. We can assume that
![]() $\langle a_\xi : \xi \in \lambda \rangle $
is strictly
$\langle a_\xi : \xi \in \lambda \rangle $
is strictly
![]() $\supseteq ^{*}$
-descending, by extracting such a subsequence. Decompose
$\supseteq ^{*}$
-descending, by extracting such a subsequence. Decompose
![]() $\mathbb {P}(E)$
as
$\mathbb {P}(E)$
as
![]() $\mathbb {P}(E^{\leq \kappa }) \times \mathbb {P}(E^{> \kappa })$
and
$\mathbb {P}(E^{\leq \kappa }) \times \mathbb {P}(E^{> \kappa })$
and
![]() ${G= G^{\leq \kappa } \times G ^{> \kappa }} $
accordingly. Since
${G= G^{\leq \kappa } \times G ^{> \kappa }} $
accordingly. Since
![]() $\mathbb {P}(E^{> \kappa })$
is
$\mathbb {P}(E^{> \kappa })$
is
![]() $\kappa ^{+}$
-closed, the
$\kappa ^{+}$
-closed, the
![]() $\mathsf {GCH}$
at
$\mathsf {GCH}$
at
![]() $\delta \leq \kappa $
still holds in
$\delta \leq \kappa $
still holds in
![]() $\mathbf {V}[G ^{> \kappa }]$
and
$\mathbf {V}[G ^{> \kappa }]$
and
![]() $(\mathbb {P}(E^{\leq \kappa }))^{\mathbf {V}[G^{{>} \kappa }]}=(\mathbb {P}(E^{\leq \kappa }))^{\mathbf {V}}$
. We designate
$(\mathbb {P}(E^{\leq \kappa }))^{\mathbf {V}[G^{{>} \kappa }]}=(\mathbb {P}(E^{\leq \kappa }))^{\mathbf {V}}$
. We designate
![]() $\mathbf {V}[G^{>\kappa }]$
as the new ground model.
$\mathbf {V}[G^{>\kappa }]$
as the new ground model.
For each
![]() $\xi \in \kappa ^{++}$
, let
$\xi \in \kappa ^{++}$
, let
![]() $\dot a_\xi $
be a nice
$\dot a_\xi $
be a nice
![]() $\mathbb {P}(E^{\leq \kappa })$
-name for
$\mathbb {P}(E^{\leq \kappa })$
-name for
![]() $a_\xi $
and let
$a_\xi $
and let
![]() $p_0 \in G^{\leq \kappa }$
be a
$p_0 \in G^{\leq \kappa }$
be a
![]() $ \mathbb {P}(E^{\leq \kappa })$
-condition such that
$ \mathbb {P}(E^{\leq \kappa })$
-condition such that
![]() $\forall \xi < \xi ' < \kappa ^{++}: p_0 \Vdash _{\mathbb {P}(E^{\leq \kappa })} {"}\dot a_\xi \supsetneq ^{*} \dot a_{\xi '}"$
.
$\forall \xi < \xi ' < \kappa ^{++}: p_0 \Vdash _{\mathbb {P}(E^{\leq \kappa })} {"}\dot a_\xi \supsetneq ^{*} \dot a_{\xi '}"$
.
Any nice
![]() $\mathbb {P}(E^{\leq \kappa })$
-name
$\mathbb {P}(E^{\leq \kappa })$
-name
![]() $\dot x$
is of the form
$\dot x$
is of the form
![]() $\dot x= \bigcup _{\alpha \in \kappa }\{\check \alpha \}\times A_\alpha (\dot x)$
, where
$\dot x= \bigcup _{\alpha \in \kappa }\{\check \alpha \}\times A_\alpha (\dot x)$
, where
![]() $A_\alpha (\dot x)$
is an antichain in
$A_\alpha (\dot x)$
is an antichain in
![]() $\mathbb {P}(E^{\leq \kappa })$
. Since
$\mathbb {P}(E^{\leq \kappa })$
. Since
![]() $\mathbb {P}(E^{\leq \kappa })$
satisfies the
$\mathbb {P}(E^{\leq \kappa })$
satisfies the
![]() $\kappa ^{+}$
-c.c., the set
$\kappa ^{+}$
-c.c., the set
 $$\begin{align*}S^\delta(\dot x):=\bigcup_{\substack{{\alpha \in \kappa}\\{p \in A_\alpha(\dot x)}}}\text{dom}(p(\delta)) \cup \text{dom}(p_0(\delta))\end{align*}$$
$$\begin{align*}S^\delta(\dot x):=\bigcup_{\substack{{\alpha \in \kappa}\\{p \in A_\alpha(\dot x)}}}\text{dom}(p(\delta)) \cup \text{dom}(p_0(\delta))\end{align*}$$
has cardinality at most
![]() $\kappa $
for every
$\kappa $
for every
![]() $\delta \in \text {dom}(E^{\leq \kappa })$
, and thus the same holds for the set
$\delta \in \text {dom}(E^{\leq \kappa })$
, and thus the same holds for the set
![]() $S(\dot x):=\bigcup _{\delta \in \text {dom}(E^{\leq \kappa })}S^\delta (\dot x)$
.
$S(\dot x):=\bigcup _{\delta \in \text {dom}(E^{\leq \kappa })}S^\delta (\dot x)$
.
By applying the
![]() $\Delta $
-system Lemma, which requires the
$\Delta $
-system Lemma, which requires the
![]() $\mathsf {GCH}$
at
$\mathsf {GCH}$
at
![]() $\kappa $
, to the family
$\kappa $
, to the family
![]() $\{S(\dot a_\xi ): \xi \in \kappa ^{++}\}$
, we find some
$\{S(\dot a_\xi ): \xi \in \kappa ^{++}\}$
, we find some
![]() $X \subseteq \kappa ^{++}$
of cardinality
$X \subseteq \kappa ^{++}$
of cardinality
![]() $\kappa ^{++}$
and a sequence
$\kappa ^{++}$
and a sequence
![]() $\langle R^\delta : \delta \in \text {dom}(E^{\leq \kappa })\rangle $
such that for all
$\langle R^\delta : \delta \in \text {dom}(E^{\leq \kappa })\rangle $
such that for all
![]() $\xi \neq \xi ' \in X$
and all
$\xi \neq \xi ' \in X$
and all
![]() $\delta \in \text {dom}(E^{\leq \kappa }): S^\delta (\dot a_\xi ) \cap S^\delta (\dot a_{\xi '})=R^\delta $
. Note that
$\delta \in \text {dom}(E^{\leq \kappa }): S^\delta (\dot a_\xi ) \cap S^\delta (\dot a_{\xi '})=R^\delta $
. Note that
![]() $\text {dom}(p_0(\delta )) \subseteq R^\delta $
. Since
$\text {dom}(p_0(\delta )) \subseteq R^\delta $
. Since
![]() $S^\delta (\dot a_\xi )$
has cardinality
$S^\delta (\dot a_\xi )$
has cardinality
![]() ${\leq }\kappa $
and since
${\leq }\kappa $
and since
![]() $\kappa ^\kappa =\kappa ^{+}$
, we find by the pigeonhole principle some
$\kappa ^\kappa =\kappa ^{+}$
, we find by the pigeonhole principle some
![]() $X'\subseteq X$
of cardinality
$X'\subseteq X$
of cardinality
![]() $\kappa ^{++}$
such that
$\kappa ^{++}$
such that
![]() $|S^\delta (\dot a_\xi )\setminus R^{\delta }|=|S^\delta (\dot a_{\xi '})\setminus R^{\delta }|$
for all
$|S^\delta (\dot a_\xi )\setminus R^{\delta }|=|S^\delta (\dot a_{\xi '})\setminus R^{\delta }|$
for all
![]() $\xi \neq \xi ' \in X'$
and
$\xi \neq \xi ' \in X'$
and
![]() $\delta \in \text {dom}(E^{\leq \kappa })$
.
$\delta \in \text {dom}(E^{\leq \kappa })$
.
Fix some
![]() $\xi _0\in X'$
and choose for each
$\xi _0\in X'$
and choose for each
![]() $\xi \in X'$
and each
$\xi \in X'$
and each
![]() $\delta \in \text {dom}(E^{\leq \kappa })$
a permutation of
$\delta \in \text {dom}(E^{\leq \kappa })$
a permutation of
![]() $E(\delta ) \times \delta $
of order 2 that maps
$E(\delta ) \times \delta $
of order 2 that maps
![]() $S^\delta (\dot a_\xi )$
to
$S^\delta (\dot a_\xi )$
to
![]() $S^\delta (\dot a_{\xi _0})$
and fixes everything besides
$S^\delta (\dot a_{\xi _0})$
and fixes everything besides
![]() $S^\delta (\dot a_\xi ) \cup S^\delta (\dot a_{\xi _0}) \setminus R^\delta $
. Denote by
$S^\delta (\dot a_\xi ) \cup S^\delta (\dot a_{\xi _0}) \setminus R^\delta $
. Denote by
![]() $\varphi ^\delta _{\xi }$
the automorphism of
$\varphi ^\delta _{\xi }$
the automorphism of
![]() $\text {Fn}_{<\delta }(E(\delta ) \times \delta , 2)$
that this permutation induces. By applying these automorphisms coordinate-wise, we obtain automorphisms of
$\text {Fn}_{<\delta }(E(\delta ) \times \delta , 2)$
that this permutation induces. By applying these automorphisms coordinate-wise, we obtain automorphisms of
![]() $\mathbb {P}(E^{\leq \kappa })$
, which we denote by
$\mathbb {P}(E^{\leq \kappa })$
, which we denote by
![]() $\varphi _{\xi }$
. Since we chose permutations fixing the
$\varphi _{\xi }$
. Since we chose permutations fixing the
![]() $R^\delta $
, we have
$R^\delta $
, we have
![]() $\varphi _\xi (p_0)=p_0$
. The automorphisms
$\varphi _\xi (p_0)=p_0$
. The automorphisms
![]() $\varphi _\xi $
extend to
$\varphi _\xi $
extend to
![]() $\mathbb {P}(E^{\leq \kappa })$
-names in the obvious way.
$\mathbb {P}(E^{\leq \kappa })$
-names in the obvious way.
Note that
![]() $\varphi _{\xi }(\dot a_\xi )$
is a nice name with
$\varphi _{\xi }(\dot a_\xi )$
is a nice name with
![]() $S(\varphi _{\xi }(\dot a_\xi )) \subseteq S(\dot a_{\xi _0})$
. By counting, we see that there are at most
$S(\varphi _{\xi }(\dot a_\xi )) \subseteq S(\dot a_{\xi _0})$
. By counting, we see that there are at most
![]() $\kappa ^{+}$
many nice names
$\kappa ^{+}$
many nice names
![]() $\dot x$
with
$\dot x$
with
![]() $S(\dot x) \subseteq S(\dot a_{\xi _0})$
. Therefore, there exists
$S(\dot x) \subseteq S(\dot a_{\xi _0})$
. Therefore, there exists
![]() $X" \subseteq X'$
of cardinality
$X" \subseteq X'$
of cardinality
![]() $\kappa ^{++}$
and a nice name
$\kappa ^{++}$
and a nice name
![]() $\dot x$
such that
$\dot x$
such that
![]() $\varphi _{\xi }(\dot a_\xi )=\dot x$
for every
$\varphi _{\xi }(\dot a_\xi )=\dot x$
for every
![]() $\xi \in X"$
.
$\xi \in X"$
.
Now, fix
![]() $\xi < \xi ' \in X"\setminus \{\xi _0\}$
and define the following automorphism of
$\xi < \xi ' \in X"\setminus \{\xi _0\}$
and define the following automorphism of
![]() $\mathbb {P}(E^{\leq \kappa })$
:
$\mathbb {P}(E^{\leq \kappa })$
:
Note that
![]() $\chi (\dot a_\xi )=\dot a_{\xi '}$
, that
$\chi (\dot a_\xi )=\dot a_{\xi '}$
, that
![]() $\chi (\dot a_{\xi '})=\dot a_{\xi }$
and that
$\chi (\dot a_{\xi '})=\dot a_{\xi }$
and that
![]() $\chi (p_0)=p_0$
. By assumption,
$\chi (p_0)=p_0$
. By assumption,
![]() $p_0 \Vdash _{\mathbb {P}(E^{\leq \kappa })} \dot a_\xi \supsetneq ^{*} \dot a_{\xi '}$
. Thus,
$p_0 \Vdash _{\mathbb {P}(E^{\leq \kappa })} \dot a_\xi \supsetneq ^{*} \dot a_{\xi '}$
. Thus,
![]() $ \chi (p_0)\Vdash _{\chi (\mathbb {P}(E^{\leq \kappa }))} \chi (\dot a_\xi ) \supsetneq ^{*} \chi (\dot a_{\xi '})$
, which implies that
$ \chi (p_0)\Vdash _{\chi (\mathbb {P}(E^{\leq \kappa }))} \chi (\dot a_\xi ) \supsetneq ^{*} \chi (\dot a_{\xi '})$
, which implies that
a contradiction.
The above result can be generalized to show that consistently, the
![]() $\kappa $
-tower spectrum equals
$\kappa $
-tower spectrum equals
![]() $\{\kappa ^{+}\}$
for all regular
$\{\kappa ^{+}\}$
for all regular
![]() $\kappa $
, while the
$\kappa $
, while the
![]() $\kappa $
-mad spectrum is arbitrarily large. More precisely, we prove the following:
$\kappa $
-mad spectrum is arbitrarily large. More precisely, we prove the following:
Theorem 2. Let
![]() $\mathbf {V}\models \mathsf {GCH}$
and let E be an index function such that for every
$\mathbf {V}\models \mathsf {GCH}$
and let E be an index function such that for every
![]() $\kappa \in \text {dom}(E)$
,
$\kappa \in \text {dom}(E)$
,
![]() $E(\kappa )$
is a closed set of cardinals with
$E(\kappa )$
is a closed set of cardinals with
![]() $\min E(\kappa )\geq \kappa ^{+}$
,
$\min E(\kappa )\geq \kappa ^{+}$
,
![]() $\text {cf}(\max E(\kappa ))> \kappa $
and such that
$\text {cf}(\max E(\kappa ))> \kappa $
and such that
![]() $\kappa < \kappa ' \implies \max E(\kappa ) \leq \max E(\kappa ')$
. There is a forcing extension of
$\kappa < \kappa ' \implies \max E(\kappa ) \leq \max E(\kappa ')$
. There is a forcing extension of
![]() $\mathbf {V}$
in which
$\mathbf {V}$
in which
This is based on a construction by Bağ, the first author and Friedman [Reference Bağ, Fischer and Friedman1]. As is shown in that paper, the same construction allows for more accurate control of
![]() $\mathfrak {sp}(\mathfrak {a}(\kappa ))$
by restricting the domain of E to successors of regular cardinals together with
$\mathfrak {sp}(\mathfrak {a}(\kappa ))$
by restricting the domain of E to successors of regular cardinals together with
![]() $\aleph _0$
, and the range of E to so-called
$\aleph _0$
, and the range of E to so-called
![]() $\kappa $
-Blass spectra. While the definition of a
$\kappa $
-Blass spectra. While the definition of a
![]() $\kappa $
-Blass spectrum is not necessary for our purposes, we give it for the sake of completeness.
$\kappa $
-Blass spectrum is not necessary for our purposes, we give it for the sake of completeness.
Definition 5 [Reference Bağ, Fischer and Friedman1, Definition 2.1]
A
![]() $\kappa $
-Blass spectrum is a set A of cardinals satisfying
$\kappa $
-Blass spectrum is a set A of cardinals satisfying
![]() $\min A=\kappa ^{+}$
,
$\min A=\kappa ^{+}$
,
![]() $\forall \mu \in A: [\text {cf}(\mu )\leq \kappa \implies \mu ^{+}\in A]$
and
$\forall \mu \in A: [\text {cf}(\mu )\leq \kappa \implies \mu ^{+}\in A]$
and
![]() $\gamma \in A$
for every cardinal
$\gamma \in A$
for every cardinal
![]() $\kappa ^{+} \leq \gamma \leq |A|$
.
$\kappa ^{+} \leq \gamma \leq |A|$
.
Corollary 1 (GCH)
If E is defined on successors of regular cardinals together with
![]() $\aleph _0$
, and
$\aleph _0$
, and
![]() $E(\kappa )$
is a
$E(\kappa )$
is a
![]() $\kappa $
-Blass spectrum for every
$\kappa $
-Blass spectrum for every
![]() $\kappa \in \text {dom}(E)$
, we consistently have
$\kappa \in \text {dom}(E)$
, we consistently have
Proof of Theorem 2
We begin by defining the relevant forcing notions.
Definition 6 [Reference Bağ, Fischer and Friedman1, Definition 4.2]
Define for each
![]() $\kappa \in \text {dom}(E)$
and each
$\kappa \in \text {dom}(E)$
and each
![]() $\lambda \in E(\kappa )$
the following forcing notion
$\lambda \in E(\kappa )$
the following forcing notion
![]() $\mathbb {A}^{\kappa , \lambda }$
: An
$\mathbb {A}^{\kappa , \lambda }$
: An
![]() $\mathbb {A}^{\kappa ,\lambda }$
-condition is a function
$\mathbb {A}^{\kappa ,\lambda }$
-condition is a function
![]() $p: \Delta ^{p} \to [\kappa ]^{{<}\kappa }$
, where
$p: \Delta ^{p} \to [\kappa ]^{{<}\kappa }$
, where
![]() $\Delta ^p \in [\lambda ]^{{<}\kappa }$
. We define
$\Delta ^p \in [\lambda ]^{{<}\kappa }$
. We define
![]() $p' \leq p$
iff:
$p' \leq p$
iff:
-
(i)
 $\Delta ^{p}\subseteq \Delta ^{p'}$
,
$\Delta ^{p}\subseteq \Delta ^{p'}$
, -
(ii)
 $\forall x \in \Delta ^{p}: p(x)\subseteq p'(x)$
,
$\forall x \in \Delta ^{p}: p(x)\subseteq p'(x)$
, -
(iii)
 $\forall \eta _1 \neq \eta _2 \in \Delta ^{p}: p'(\eta _1)\cap p'(\eta _2)\subseteq p(\eta _1)\cap p(\eta _2)$
.
$\forall \eta _1 \neq \eta _2 \in \Delta ^{p}: p'(\eta _1)\cap p'(\eta _2)\subseteq p(\eta _1)\cap p(\eta _2)$
.
For each
![]() $\kappa \in \text {dom}(E)$
, let
$\kappa \in \text {dom}(E)$
, let
![]() $\mathbb {A}^\kappa $
be the
$\mathbb {A}^\kappa $
be the
![]() ${<}\kappa $
-support product of the
${<}\kappa $
-support product of the
![]() $\mathbb {A}^{\kappa ,\lambda }$
over all
$\mathbb {A}^{\kappa ,\lambda }$
over all
![]() $\lambda \in E(\kappa )$
. Then, let
$\lambda \in E(\kappa )$
. Then, let
![]() $\mathbb {A}$
be the Easton-product of the
$\mathbb {A}$
be the Easton-product of the
![]() $\mathbb {A}^\kappa $
.
$\mathbb {A}^\kappa $
.
Let G be
![]() $\mathbb {A}$
-generic over
$\mathbb {A}$
-generic over
![]() $\mathbf {V}$
. It is shown in [Reference Bağ, Fischer and Friedman1, Theorem 4.6 and Remark 4.7] that for all
$\mathbf {V}$
. It is shown in [Reference Bağ, Fischer and Friedman1, Theorem 4.6 and Remark 4.7] that for all
![]() $\kappa \in \text {dom}(E): E(\kappa )\subseteq \mathfrak {sp}(\mathfrak {a}(\kappa ))$
and
$\kappa \in \text {dom}(E): E(\kappa )\subseteq \mathfrak {sp}(\mathfrak {a}(\kappa ))$
and
![]() $2^\kappa =\max E(\kappa )$
holds in
$2^\kappa =\max E(\kappa )$
holds in
![]() $\mathbf {V}[G]$
. To show the other equality, let
$\mathbf {V}[G]$
. To show the other equality, let
![]() $\kappa \in \text {dom}(E)$
and decompose
$\kappa \in \text {dom}(E)$
and decompose
![]() $\mathbb {A}$
as
$\mathbb {A}$
as
![]() $\mathbb {A}^{{>}\kappa }\times \mathbb {A}^{\leq \kappa }$
and
$\mathbb {A}^{{>}\kappa }\times \mathbb {A}^{\leq \kappa }$
and
![]() $G=G^{{>}\kappa }\times G^{\leq \kappa }$
accordingly. As is shown in [Reference Bağ, Fischer and Friedman1, Lemma 4.3],
$G=G^{{>}\kappa }\times G^{\leq \kappa }$
accordingly. As is shown in [Reference Bağ, Fischer and Friedman1, Lemma 4.3],
![]() $\mathbb {A}^{{>}\kappa }$
is
$\mathbb {A}^{{>}\kappa }$
is
![]() $\kappa ^{+}$
-closed and
$\kappa ^{+}$
-closed and
![]() $\mathbb {A}^{\leq \kappa }$
satisfies the
$\mathbb {A}^{\leq \kappa }$
satisfies the
![]() $\kappa ^{+}$
-c.c., which implies that the
$\kappa ^{+}$
-c.c., which implies that the
![]() $\mathsf {GCH}$
at
$\mathsf {GCH}$
at
![]() $\delta \leq \kappa $
still holds in
$\delta \leq \kappa $
still holds in
![]() $\mathbf {V}[G^{{>}\kappa }]$
and that
$\mathbf {V}[G^{{>}\kappa }]$
and that
![]() $(\mathbb {A}^{\leq \kappa })^{\mathbf {V}[G^{{>}\kappa }]}=(\mathbb {A}^{\leq \kappa })^{\mathbf {V}}$
. Let
$(\mathbb {A}^{\leq \kappa })^{\mathbf {V}[G^{{>}\kappa }]}=(\mathbb {A}^{\leq \kappa })^{\mathbf {V}}$
. Let
![]() $\mathbf {W}:=\mathbf {V}[G^{{>}\kappa }]$
be the new ground model.
$\mathbf {W}:=\mathbf {V}[G^{{>}\kappa }]$
be the new ground model.
Assume by contradiction that
![]() $\langle a_\xi : \xi < \kappa ^{++}\rangle $
is a strictly
$\langle a_\xi : \xi < \kappa ^{++}\rangle $
is a strictly
![]() $\supseteq ^{*}$
-descending sequence of cofinal subsets of
$\supseteq ^{*}$
-descending sequence of cofinal subsets of
![]() $\kappa $
in
$\kappa $
in
![]() $\mathbf {W}[G^{\leq \kappa }]$
. Let
$\mathbf {W}[G^{\leq \kappa }]$
. Let
![]() $\dot a_\xi $
be a nice
$\dot a_\xi $
be a nice
![]() $\mathbb {A}^{\leq \kappa }$
-name for
$\mathbb {A}^{\leq \kappa }$
-name for
![]() $a_\xi $
and let
$a_\xi $
and let
![]() $p_0$
be such that for all
$p_0$
be such that for all
![]() $\xi < \xi ' < \kappa ^{++}: p_0\Vdash \dot a_\xi \supsetneq ^{*} \dot a_{\xi '}$
.
$\xi < \xi ' < \kappa ^{++}: p_0\Vdash \dot a_\xi \supsetneq ^{*} \dot a_{\xi '}$
.
In order to find the required isomorphisms, we must first extend the forcing notion
![]() $\mathbb {A}^{\leq \kappa }$
to a larger forcing notion
$\mathbb {A}^{\leq \kappa }$
to a larger forcing notion
![]() $\mathbb {Q}^{\leq \kappa }$
into which
$\mathbb {Q}^{\leq \kappa }$
into which
![]() $\mathbb {A}^{\leq \kappa }$
completely embeds.
$\mathbb {A}^{\leq \kappa }$
completely embeds.
Definition 7. For every
![]() $\delta \in \text {dom}(E^{\leq \kappa })$
, let
$\delta \in \text {dom}(E^{\leq \kappa })$
, let
![]() $b^\delta :=|E(\delta )|$
and
$b^\delta :=|E(\delta )|$
and
![]() $J^\delta :=\max E(\delta )$
, and for every
$J^\delta :=\max E(\delta )$
, and for every
![]() $\beta \in b^\delta $
, let
$\beta \in b^\delta $
, let
![]() $\mathbb {Q}^{\delta ,\beta }$
be the forcing notion
$\mathbb {Q}^{\delta ,\beta }$
be the forcing notion
![]() $\mathbb {A}^{\delta , J_\delta }$
. Let
$\mathbb {A}^{\delta , J_\delta }$
. Let
![]() $\mathbb {Q}^{\delta }$
be the
$\mathbb {Q}^{\delta }$
be the
![]() ${<}\kappa $
-support product of the
${<}\kappa $
-support product of the
![]() $\mathbb {Q}^{\delta , \beta }$
and
$\mathbb {Q}^{\delta , \beta }$
and
![]() $\mathbb {Q}^{\leq \kappa }$
the Easton-product over all
$\mathbb {Q}^{\leq \kappa }$
the Easton-product over all
![]() $\delta \in \text {dom}(E^{\leq \kappa })$
of the
$\delta \in \text {dom}(E^{\leq \kappa })$
of the
![]() $\mathbb {Q}^{\delta }$
.
$\mathbb {Q}^{\delta }$
.
It is easy to verify that
![]() $\mathbb {A}^{\leq \kappa }$
completely embeds into
$\mathbb {A}^{\leq \kappa }$
completely embeds into
![]() $\mathbb {Q}^{\leq \kappa }$
(see [Reference Bağ, Fischer and Friedman1, Lemma 4.8]). Thus,
$\mathbb {Q}^{\leq \kappa }$
(see [Reference Bağ, Fischer and Friedman1, Lemma 4.8]). Thus,
![]() $\forall \xi < \xi ' < \kappa ^{++}:p_0 \Vdash _{\mathbb {Q}^{\leq \kappa }} \dot a_\xi \supsetneq ^{*} \dot a_{\xi '}$
.
$\forall \xi < \xi ' < \kappa ^{++}:p_0 \Vdash _{\mathbb {Q}^{\leq \kappa }} \dot a_\xi \supsetneq ^{*} \dot a_{\xi '}$
.
Definition 8. Let
![]() $\dot x$
be a nice
$\dot x$
be a nice
![]() $\mathbb {Q}^{\leq \kappa }$
-name for a subset of
$\mathbb {Q}^{\leq \kappa }$
-name for a subset of
![]() $\kappa $
, i.e.,
$\kappa $
, i.e.,
![]() $\dot x = \bigcup _{\alpha \in \kappa }\{\check \alpha \} \times A_\alpha (\dot x)$
. For each
$\dot x = \bigcup _{\alpha \in \kappa }\{\check \alpha \} \times A_\alpha (\dot x)$
. For each
![]() $\delta \in \text {dom}(E^{\leq \kappa })$
and
$\delta \in \text {dom}(E^{\leq \kappa })$
and
![]() $\beta \in b^\delta $
, define the following sets:
$\beta \in b^\delta $
, define the following sets:
 $$\begin{align*}\begin{aligned} \text{supp}^{\delta}(\dot x) &:= \bigcup_{\substack{{\alpha \in \kappa}\\p \in A_\alpha(\dot x)}}\text{supp}(p(\delta)) \cup \text{supp}(p_0(\delta)) \in [b^\delta]^{\leq \kappa}\\ \Delta^{\delta, \beta}(\dot x)&:= \bigcup_{\substack{{\alpha \in \kappa}\\p \in A_\alpha(\dot x)}}\Delta^{p(\delta)(\beta)} \cup \Delta^{p_0(\delta)(\beta)}\in [J^{\delta}]^{\leq \kappa.} \end{aligned} \end{align*}$$
$$\begin{align*}\begin{aligned} \text{supp}^{\delta}(\dot x) &:= \bigcup_{\substack{{\alpha \in \kappa}\\p \in A_\alpha(\dot x)}}\text{supp}(p(\delta)) \cup \text{supp}(p_0(\delta)) \in [b^\delta]^{\leq \kappa}\\ \Delta^{\delta, \beta}(\dot x)&:= \bigcup_{\substack{{\alpha \in \kappa}\\p \in A_\alpha(\dot x)}}\Delta^{p(\delta)(\beta)} \cup \Delta^{p_0(\delta)(\beta)}\in [J^{\delta}]^{\leq \kappa.} \end{aligned} \end{align*}$$
By applying the
![]() $\Delta $
-system Lemma, we obtain some
$\Delta $
-system Lemma, we obtain some
![]() $X \subseteq \kappa ^{++}$
of cardinality
$X \subseteq \kappa ^{++}$
of cardinality
![]() $\kappa ^{++}$
and for each
$\kappa ^{++}$
and for each
![]() $\delta \in \text {dom}(E^{\leq \kappa })$
a root
$\delta \in \text {dom}(E^{\leq \kappa })$
a root
![]() $R^\delta $
such that for all
$R^\delta $
such that for all
![]() $\xi \neq \xi ' \in X: \text {supp}^{\delta }(\dot a_\xi )\cap \text {supp}^{\delta }(\dot a_{\xi '})=R^\delta $
. Since
$\xi \neq \xi ' \in X: \text {supp}^{\delta }(\dot a_\xi )\cap \text {supp}^{\delta }(\dot a_{\xi '})=R^\delta $
. Since
![]() $\kappa ^\kappa =\kappa ^{+}< \kappa ^{++}$
, we can assume without loss of generality that for every
$\kappa ^\kappa =\kappa ^{+}< \kappa ^{++}$
, we can assume without loss of generality that for every
![]() $\delta \in \text {dom}(E^{\leq \kappa })$
, the value
$\delta \in \text {dom}(E^{\leq \kappa })$
, the value
![]() $|\text {supp}^{\delta }(\dot a_\xi )\setminus R^\delta |$
does not depend on
$|\text {supp}^{\delta }(\dot a_\xi )\setminus R^\delta |$
does not depend on
![]() $\xi \in X$
.
$\xi \in X$
.
Fix some
![]() $\xi _0\in X$
and let
$\xi _0\in X$
and let
![]() $\psi ^\delta _\xi $
be a permutation of
$\psi ^\delta _\xi $
be a permutation of
![]() $b^\delta $
of order 2 that maps
$b^\delta $
of order 2 that maps
![]() $\text {supp}^{\delta }(\dot a_\xi )$
to
$\text {supp}^{\delta }(\dot a_\xi )$
to
![]() $\text {supp}^{\delta }(\dot a_{\xi _0})$
and fixes everything outside of
$\text {supp}^{\delta }(\dot a_{\xi _0})$
and fixes everything outside of
![]() $(\text {supp}^{\delta }(\dot a_\xi )\cup \text {supp}^{\delta }(\dot a_{\xi _0})) \setminus R^\delta $
. This permutation naturally induces an automorphisms of
$(\text {supp}^{\delta }(\dot a_\xi )\cup \text {supp}^{\delta }(\dot a_{\xi _0})) \setminus R^\delta $
. This permutation naturally induces an automorphisms of
![]() $\mathbb {Q^\delta }$
. By applying these automorphisms coordinate-wise, we obtain for each
$\mathbb {Q^\delta }$
. By applying these automorphisms coordinate-wise, we obtain for each
![]() $\xi \in X$
an automorphism of the entire
$\xi \in X$
an automorphism of the entire
![]() $\mathbb {Q}^{\leq \kappa }$
, which we call
$\mathbb {Q}^{\leq \kappa }$
, which we call
![]() $\psi _\xi $
. It recursively extends to
$\psi _\xi $
. It recursively extends to
![]() $\mathbb {Q}^{\leq \kappa }$
-names. Note that
$\mathbb {Q}^{\leq \kappa }$
-names. Note that
![]() $\forall \delta \in \text {dom}(E^{\leq \kappa }): \text {supp}^{\delta }(\psi _\xi (\dot a_\xi ))=\text {supp}^{\delta }(\dot a_{\xi _0})$
,
$\forall \delta \in \text {dom}(E^{\leq \kappa }): \text {supp}^{\delta }(\psi _\xi (\dot a_\xi ))=\text {supp}^{\delta }(\dot a_{\xi _0})$
,
![]() $\psi _\xi (p_0)=p_0$
and for every
$\psi _\xi (p_0)=p_0$
and for every
![]() ${\xi '\in X\setminus \{\xi , \xi _0\}: \psi _\xi (\dot a_{\xi '})=\dot a_{\xi '}}$
.
${\xi '\in X\setminus \{\xi , \xi _0\}: \psi _\xi (\dot a_{\xi '})=\dot a_{\xi '}}$
.
In an abuse of notation, we assume that the sets
![]() $J^\delta $
underlying the forcing notions
$J^\delta $
underlying the forcing notions
![]() $\mathbb {Q}^{\delta ,\beta }$
are disjoint for different
$\mathbb {Q}^{\delta ,\beta }$
are disjoint for different
![]() $(\delta , \beta )$
and apply the
$(\delta , \beta )$
and apply the
![]() $\Delta $
-system Lemma to the family
$\Delta $
-system Lemma to the family
We obtain some
![]() $X'\subseteq X$
of cardinality
$X'\subseteq X$
of cardinality
![]() $\kappa ^{++}$
and for each
$\kappa ^{++}$
and for each
![]() $\delta \in \text {dom}(E^{\leq \kappa })$
and each
$\delta \in \text {dom}(E^{\leq \kappa })$
and each
![]() $\beta \in b^\delta $
a root
$\beta \in b^\delta $
a root
![]() $R^{\delta , \beta }$
, i.e., we have for all
$R^{\delta , \beta }$
, i.e., we have for all
![]() $\xi \neq \xi ' \in X'$
, every
$\xi \neq \xi ' \in X'$
, every
![]() $\delta \in \text {dom}(E^{\leq \kappa })$
and every
$\delta \in \text {dom}(E^{\leq \kappa })$
and every
![]() $\beta \in b^\delta $
:
$\beta \in b^\delta $
:
![]() $\Delta ^{\delta , \beta }(\psi _\xi (\dot a_\xi ))\cap \Delta ^{\delta , \beta }(\psi _{\xi '}(\dot a_{\xi '}))=R^{\delta , \beta }$
.
$\Delta ^{\delta , \beta }(\psi _\xi (\dot a_\xi ))\cap \Delta ^{\delta , \beta }(\psi _{\xi '}(\dot a_{\xi '}))=R^{\delta , \beta }$
.
Since
![]() $\text {supp}^{\delta }(\psi _\xi (\dot a_\xi ))=\text {supp}^{\delta }(\dot a_{\xi _0})$
, and since
$\text {supp}^{\delta }(\psi _\xi (\dot a_\xi ))=\text {supp}^{\delta }(\dot a_{\xi _0})$
, and since
![]() $\kappa ^\kappa < \kappa ^{++}$
, we can again assume without loss of generality that the value
$\kappa ^\kappa < \kappa ^{++}$
, we can again assume without loss of generality that the value
![]() $|\Delta ^{\delta , \beta }(\psi _\xi (\dot a_\xi ))\setminus R^{\delta , \beta }|$
does not depend on
$|\Delta ^{\delta , \beta }(\psi _\xi (\dot a_\xi ))\setminus R^{\delta , \beta }|$
does not depend on
![]() $\xi \in X'$
. We may therefore fix
$\xi \in X'$
. We may therefore fix
![]() $\xi _1 \in X'$
and choose for each
$\xi _1 \in X'$
and choose for each
![]() $\delta \in \text {dom}(E^{\leq \kappa })$
and
$\delta \in \text {dom}(E^{\leq \kappa })$
and
![]() $\beta \in b^\delta $
some permutation
$\beta \in b^\delta $
some permutation
![]() $\varphi ^{\delta , \beta }_\xi $
of order 2 of
$\varphi ^{\delta , \beta }_\xi $
of order 2 of
![]() $J^{\delta }$
that maps
$J^{\delta }$
that maps
![]() $\Delta ^{\delta , \beta }(\psi _\xi (\dot a _\xi ))$
to
$\Delta ^{\delta , \beta }(\psi _\xi (\dot a _\xi ))$
to
![]() $\Delta ^{\delta , \beta }(\psi _{\xi _1}(\dot a _{\xi _1}))$
, and fixes everything except for
$\Delta ^{\delta , \beta }(\psi _{\xi _1}(\dot a _{\xi _1}))$
, and fixes everything except for
![]() $(\Delta ^{\delta , \beta }(\psi _\xi (\dot a _\xi )) \cup \Delta ^{\delta , \beta }(\psi _{\xi _1}(\dot a _{\xi _1})))\setminus R^{\delta , \beta }$
. This map induces an automorphism of
$(\Delta ^{\delta , \beta }(\psi _\xi (\dot a _\xi )) \cup \Delta ^{\delta , \beta }(\psi _{\xi _1}(\dot a _{\xi _1})))\setminus R^{\delta , \beta }$
. This map induces an automorphism of
![]() $\mathbb {Q}^{\delta , \beta }$
, and by applying the maps coordinate-wise, we again obtain an automorphism of the entire
$\mathbb {Q}^{\delta , \beta }$
, and by applying the maps coordinate-wise, we again obtain an automorphism of the entire
![]() $\mathbb {Q}^{\leq \kappa }$
, which we denote by
$\mathbb {Q}^{\leq \kappa }$
, which we denote by
![]() $\varphi _\xi $
. Note that
$\varphi _\xi $
. Note that
![]() $\varphi _\xi (p_0)=p_0$
and for every
$\varphi _\xi (p_0)=p_0$
and for every
![]() $\xi ' \in X'\setminus \{\xi ,\xi _1\}: \varphi _\xi (\dot a_{\xi '})= \dot a_{\xi '}.$
$\xi ' \in X'\setminus \{\xi ,\xi _1\}: \varphi _\xi (\dot a_{\xi '})= \dot a_{\xi '}.$
By definition of the maps,
![]() $\varphi _\xi \circ \psi _\xi (\dot a_\xi )$
is a nice name satisfying for every
$\varphi _\xi \circ \psi _\xi (\dot a_\xi )$
is a nice name satisfying for every
![]() ${\delta \in \text {dom}(E^{\leq \kappa })}$
and
${\delta \in \text {dom}(E^{\leq \kappa })}$
and
![]() $\beta \in b^\delta $
:
$\beta \in b^\delta $
:
By an easy counting argument, there are at most
![]() $\kappa ^{+}$
many nice names with this property, which implies that there exist fixed
$\kappa ^{+}$
many nice names with this property, which implies that there exist fixed
![]() $\xi \neq \xi ' \in X'\setminus \{\xi _0, \xi _1\}$
and a nice name
$\xi \neq \xi ' \in X'\setminus \{\xi _0, \xi _1\}$
and a nice name
![]() $\dot z$
such that
$\dot z$
such that
![]() $\varphi _\xi \circ \psi _\xi (\dot a_\xi ) = \varphi _{\xi '} \circ \psi _{\xi '}(\dot a_{\xi '})=\dot z$
.
$\varphi _\xi \circ \psi _\xi (\dot a_\xi ) = \varphi _{\xi '} \circ \psi _{\xi '}(\dot a_{\xi '})=\dot z$
.
Since we have fixed
![]() $\xi $
and
$\xi $
and
![]() $\xi '$
, we will from now on use the shorthands
$\xi '$
, we will from now on use the shorthands
![]() ${\psi :=\psi _\xi ,\; \psi ':=\psi _{\xi '},\; \varphi :=\varphi _\xi , \;\varphi ':=\varphi _{\xi '}}$
. The rest of the proof consists in showing that the automorphism
${\psi :=\psi _\xi ,\; \psi ':=\psi _{\xi '},\; \varphi :=\varphi _\xi , \;\varphi ':=\varphi _{\xi '}}$
. The rest of the proof consists in showing that the automorphism
satisfies
![]() $\chi (\dot a_\xi )=\dot a_{\xi '}$
and
$\chi (\dot a_\xi )=\dot a_{\xi '}$
and
![]() $\chi (\dot a_{\xi '})=\dot a_{\xi }$
. Unfortunately, there does not seem to be a shorter one that works. Since
$\chi (\dot a_{\xi '})=\dot a_{\xi }$
. Unfortunately, there does not seem to be a shorter one that works. Since
![]() $\chi (p_0)=p_0$
, we obtain the contradiction
$\chi (p_0)=p_0$
, we obtain the contradiction
just as in the proof of Theorem 1.
Definition 9. Let
![]() $U^{\delta }:=\text {supp}^{\delta }(\dot a_{\xi _0}), \;U^{\delta , \beta }:=\Delta ^{\delta , \beta }(\psi _{\xi _1}(\dot a_{\xi _1}))$
and define the following subsets of
$U^{\delta }:=\text {supp}^{\delta }(\dot a_{\xi _0}), \;U^{\delta , \beta }:=\Delta ^{\delta , \beta }(\psi _{\xi _1}(\dot a_{\xi _1}))$
and define the following subsets of
![]() $\mathbb {Q^{\leq \kappa }}$
:
$\mathbb {Q^{\leq \kappa }}$
:
-
(i)
 $\mathbb {R}^{\mathsf {R}}:=\{p \in \mathbb {Q}^{\leq \kappa }: \forall \delta \in \text {dom}(E^{\leq \kappa })\;\forall \beta \in b^\delta : \text {supp}(p(\delta ))\subseteq R^{\delta } \land \Delta ^{p(\delta )(\beta )}\subseteq R^{\delta , \beta }\}.$
$\mathbb {R}^{\mathsf {R}}:=\{p \in \mathbb {Q}^{\leq \kappa }: \forall \delta \in \text {dom}(E^{\leq \kappa })\;\forall \beta \in b^\delta : \text {supp}(p(\delta ))\subseteq R^{\delta } \land \Delta ^{p(\delta )(\beta )}\subseteq R^{\delta , \beta }\}.$
-
(ii)
 $\mathbb {R}^{\mathsf {U}}:=\{p \in \mathbb {Q}^{\leq \kappa }: \forall \delta \in \text {dom}(E^{\leq \kappa })\,\forall \beta \in b^\delta : \text {supp}(p(\delta ))\subseteq R^{\delta } \land \Delta ^{p(\delta )(\beta )}\subseteq U^{\delta , \beta } \setminus R^{\delta , \beta }\}.$
$\mathbb {R}^{\mathsf {U}}:=\{p \in \mathbb {Q}^{\leq \kappa }: \forall \delta \in \text {dom}(E^{\leq \kappa })\,\forall \beta \in b^\delta : \text {supp}(p(\delta ))\subseteq R^{\delta } \land \Delta ^{p(\delta )(\beta )}\subseteq U^{\delta , \beta } \setminus R^{\delta , \beta }\}.$
-
(iii)
 $\mathbb {R}^{\xi }:=\{p \in \mathbb {Q}^{\leq \kappa }: \forall \delta \in \text {dom}(E^{\leq \kappa })\,\forall \beta \in b^\delta : \text {supp}(p(\delta ))\subseteq R^{\delta } \land \Delta ^{p(\delta )(\beta )}\subseteq \Delta ^{\delta , \beta }(\dot a_\xi )\setminus R^{\delta , \beta } \}$
, and define
$\mathbb {R}^{\xi }:=\{p \in \mathbb {Q}^{\leq \kappa }: \forall \delta \in \text {dom}(E^{\leq \kappa })\,\forall \beta \in b^\delta : \text {supp}(p(\delta ))\subseteq R^{\delta } \land \Delta ^{p(\delta )(\beta )}\subseteq \Delta ^{\delta , \beta }(\dot a_\xi )\setminus R^{\delta , \beta } \}$
, and define
 $\mathbb {R}^{\xi '}$
analogously.
$\mathbb {R}^{\xi '}$
analogously. -
(iv)
 $\mathbb {U}:= \{p \in \mathbb {Q}^{\leq \kappa }: \forall \delta \in \text {dom}(E^{\leq \kappa }): \text {supp}(p(\delta ))\subseteq U^{\delta }\setminus R^{\delta }\}.$
$\mathbb {U}:= \{p \in \mathbb {Q}^{\leq \kappa }: \forall \delta \in \text {dom}(E^{\leq \kappa }): \text {supp}(p(\delta ))\subseteq U^{\delta }\setminus R^{\delta }\}.$
-
(v)
 $\mathbb {P}^\xi :=\{p \in \mathbb {Q}^{\leq \kappa }: \forall \delta \in \text {dom}(E^{\leq \kappa }): \text {supp}(p(\delta ))\subseteq \text {supp}^{\delta }(\dot a_\xi )\setminus R^\delta \}$
, and define
$\mathbb {P}^\xi :=\{p \in \mathbb {Q}^{\leq \kappa }: \forall \delta \in \text {dom}(E^{\leq \kappa }): \text {supp}(p(\delta ))\subseteq \text {supp}^{\delta }(\dot a_\xi )\setminus R^\delta \}$
, and define
 $\mathbb {P}^{\xi '}$
analogously.
$\mathbb {P}^{\xi '}$
analogously. -
(vi))
 $\mathbb {S}^\xi :=\{p \in \mathbb {Q}^{\leq \kappa }: \forall \delta \in \text {dom}(E^{\leq \kappa })\,\forall \beta \in R^{\delta }: \text {supp}(p(\delta ))\subseteq \text {supp}^{\delta }(\dot a_\xi ) \land \Delta ^{p(\delta )(\beta )} \subseteq \Delta ^{\delta , \beta }(\dot a_\xi )\}$
, and define
$\mathbb {S}^\xi :=\{p \in \mathbb {Q}^{\leq \kappa }: \forall \delta \in \text {dom}(E^{\leq \kappa })\,\forall \beta \in R^{\delta }: \text {supp}(p(\delta ))\subseteq \text {supp}^{\delta }(\dot a_\xi ) \land \Delta ^{p(\delta )(\beta )} \subseteq \Delta ^{\delta , \beta }(\dot a_\xi )\}$
, and define
 $\mathbb {S}^{\xi '}$
analogously.
$\mathbb {S}^{\xi '}$
analogously.
Figure 1 The supports at coordinate
 $\delta \in \text {dom}(E^{\leq \kappa })$
of conditions in the sets defined in Definition 9, and how the maps
$\delta \in \text {dom}(E^{\leq \kappa })$
of conditions in the sets defined in Definition 9, and how the maps
 $\varphi , \psi , \varphi '$
and
$\varphi , \psi , \varphi '$
and
 $\psi '$
act on these sets. Note that conditions in
$\psi '$
act on these sets. Note that conditions in
 $\mathbb {S}^\xi $
live in the union of the regions labeled
$\mathbb {S}^\xi $
live in the union of the regions labeled
 $\mathbb {P}^\xi , \mathbb {R}^\xi ,$
and
$\mathbb {P}^\xi , \mathbb {R}^\xi ,$
and
 $\mathbb {R}^{\mathsf {R}}$
(and analogously for
$\mathbb {R}^{\mathsf {R}}$
(and analogously for
 $\mathbb {S}^{\xi '}$
).
$\mathbb {S}^{\xi '}$
).
These sets, as well as the actions of
![]() $\varphi , \psi , \varphi '$
and
$\varphi , \psi , \varphi '$
and
![]() $\psi '$
on them, are depicted in Figure 1. Note that
$\psi '$
on them, are depicted in Figure 1. Note that
![]() $\mathbb {R}^{\mathsf {R}} \cup \mathbb {R}^\xi \cup \mathbb {P}^\xi \subseteq \mathbb {S}^\xi $
.
$\mathbb {R}^{\mathsf {R}} \cup \mathbb {R}^\xi \cup \mathbb {P}^\xi \subseteq \mathbb {S}^\xi $
.
Fact 3. The following properties are very easy to verify.
-
(i)
 $\psi |_{\mathbb {R}^{\mathsf {R}}}=\psi |_{\mathbb {R}^{\mathsf {U}}}=\psi |_{\mathbb {R}^\xi }=\text {id}$
, and the same for
$\psi |_{\mathbb {R}^{\mathsf {R}}}=\psi |_{\mathbb {R}^{\mathsf {U}}}=\psi |_{\mathbb {R}^\xi }=\text {id}$
, and the same for
 $\psi '$
in place of
$\psi '$
in place of
 $\psi $
.
$\psi $
. -
(ii)
 $\psi [\mathbb {U}] = \mathbb {P}^\xi $
, and analogously
$\psi [\mathbb {U}] = \mathbb {P}^\xi $
, and analogously
 $\psi '[\mathbb {U}] = \mathbb {P}^{\xi '}$
.
$\psi '[\mathbb {U}] = \mathbb {P}^{\xi '}$
. -
(iii)
 $\varphi |_{\mathbb {R}^{\mathsf {R}}}=\text {id}$
, and the same for
$\varphi |_{\mathbb {R}^{\mathsf {R}}}=\text {id}$
, and the same for
 $\varphi '$
in place of
$\varphi '$
in place of
 $\varphi $
.
$\varphi $
. -
(iv)
 $\varphi [\mathbb {R}^{\mathsf {U}}] = \mathbb {R}^\xi $
, and analogously
$\varphi [\mathbb {R}^{\mathsf {U}}] = \mathbb {R}^\xi $
, and analogously
 $\varphi '[\mathbb {R}^{\mathsf {U}}] = \mathbb {R}^{\xi '}$
.
$\varphi '[\mathbb {R}^{\mathsf {U}}] = \mathbb {R}^{\xi '}$
. -
(v)
 $\psi |_{\mathbb {S}^{\xi '}}=\text {id}$
, and analogously
$\psi |_{\mathbb {S}^{\xi '}}=\text {id}$
, and analogously
 $\psi '|_{\mathbb {S}^{\xi }}=\text {id}$
.
$\psi '|_{\mathbb {S}^{\xi }}=\text {id}$
. -
(vi)
 $\varphi |_{\mathbb {S}^{\xi '}}=\text {id}$
, and analogously
$\varphi |_{\mathbb {S}^{\xi '}}=\text {id}$
, and analogously
 $\varphi '|_{\mathbb {S}^{\xi }}=\text {id}$
.
$\varphi '|_{\mathbb {S}^{\xi }}=\text {id}$
. -
(vii)
 $\varphi |_{\mathbb {P}^\xi }=\text {id}$
, and analogously
$\varphi |_{\mathbb {P}^\xi }=\text {id}$
, and analogously
 $\varphi '|_{\mathbb {P}^{\xi '}}=\text {id}$
.
$\varphi '|_{\mathbb {P}^{\xi '}}=\text {id}$
.
Definition 10. Let
![]() $\delta \in \text {dom}(E^{\leq \kappa })$
and let q and
$\delta \in \text {dom}(E^{\leq \kappa })$
and let q and
![]() $q'$
be
$q'$
be
![]() $\mathbb {Q}^{\delta }$
-conditions such that for all
$\mathbb {Q}^{\delta }$
-conditions such that for all
![]() $\beta \in b^\delta : \Delta ^{q(\delta )(\beta )}\cap \Delta ^{q'(\delta )(\beta )} = \emptyset $
. We define the condition
$\beta \in b^\delta : \Delta ^{q(\delta )(\beta )}\cap \Delta ^{q'(\delta )(\beta )} = \emptyset $
. We define the condition
![]() $q + q' := \langle q(\delta )(\beta )\cup q'(\delta )(\beta ): \beta \in b^\delta \rangle $
.
$q + q' := \langle q(\delta )(\beta )\cup q'(\delta )(\beta ): \beta \in b^\delta \rangle $
.
Furthermore, if p and
![]() $p'$
are
$p'$
are
![]() $\mathbb {Q}^{\leq \kappa }$
conditions such that for all
$\mathbb {Q}^{\leq \kappa }$
conditions such that for all
![]() $\delta \in \text {dom}(E^{\leq \kappa })$
and all
$\delta \in \text {dom}(E^{\leq \kappa })$
and all
![]() $\beta \in b^\delta : \Delta ^{q(\delta )(\beta )}\cap \Delta ^{q'(\delta )(\beta )} = \emptyset $
, we define
$\beta \in b^\delta : \Delta ^{q(\delta )(\beta )}\cap \Delta ^{q'(\delta )(\beta )} = \emptyset $
, we define
Fact 4. For every
![]() $\theta \in \{\psi , \varphi , \psi ', \varphi '\}: \theta (p \oplus p')= \theta (p)\oplus \theta (p')$
.
$\theta \in \{\psi , \varphi , \psi ', \varphi '\}: \theta (p \oplus p')= \theta (p)\oplus \theta (p')$
.
Recall that the nice name
![]() $\dot z$
is of the form
$\dot z$
is of the form
![]() $\dot z=\bigcup _{\alpha \in \kappa }\{\check \alpha \}\times A_\alpha (\dot z)$
. Let
$\dot z=\bigcup _{\alpha \in \kappa }\{\check \alpha \}\times A_\alpha (\dot z)$
. Let
![]() $\alpha \in \kappa $
and
$\alpha \in \kappa $
and
![]() $q \in A_\alpha (\dot z)$
. By construction, for every
$q \in A_\alpha (\dot z)$
. By construction, for every
![]() $\delta \in \text {dom}(E^{\leq \kappa }): \text {supp}(q(\delta ))\subseteq U^{\delta }$
. We can therefore decompose q as
$\delta \in \text {dom}(E^{\leq \kappa }): \text {supp}(q(\delta ))\subseteq U^{\delta }$
. We can therefore decompose q as
![]() $q=\bar q \oplus u$
, where for every
$q=\bar q \oplus u$
, where for every
![]() $\delta \in \text {dom}(E^{\leq \kappa }): \text {supp}(\bar q(\delta ))\subseteq R^\delta $
and
$\delta \in \text {dom}(E^{\leq \kappa }): \text {supp}(\bar q(\delta ))\subseteq R^\delta $
and
![]() $\text {supp}(u(\delta ))\subseteq U^\delta \setminus R^\delta $
. Again by construction, we have for every
$\text {supp}(u(\delta ))\subseteq U^\delta \setminus R^\delta $
. Again by construction, we have for every
![]() $\beta \in b^\delta : \Delta ^{q(\delta )(\beta )} \subseteq U^{\delta , \beta }$
. We can thus further decompose
$\beta \in b^\delta : \Delta ^{q(\delta )(\beta )} \subseteq U^{\delta , \beta }$
. We can thus further decompose
![]() $\bar q$
as
$\bar q$
as
![]() $q^{\mathsf {R}} \oplus q^{\mathsf {U}}$
, where
$q^{\mathsf {R}} \oplus q^{\mathsf {U}}$
, where
![]() $\Delta ^{q^{\mathsf {R}}(\delta )(\beta )}\subseteq R^{\delta , \beta }$
and
$\Delta ^{q^{\mathsf {R}}(\delta )(\beta )}\subseteq R^{\delta , \beta }$
and
![]() $\Delta ^{q^{\mathsf {U}}(\delta )(\beta )} \subseteq U^{\delta , \beta }\setminus R^{\delta , \beta }$
.
$\Delta ^{q^{\mathsf {U}}(\delta )(\beta )} \subseteq U^{\delta , \beta }\setminus R^{\delta , \beta }$
.
This gives us a decomposition
![]() $q=q^{\mathsf {R}} \oplus q^{\mathsf {U}} \oplus u$
, where
$q=q^{\mathsf {R}} \oplus q^{\mathsf {U}} \oplus u$
, where
![]() $q^{\mathsf {R}} \in \mathbb {R}^{\mathsf {R}}$
,
$q^{\mathsf {R}} \in \mathbb {R}^{\mathsf {R}}$
,
![]() $q^{\mathsf {U}} \in \mathbb {R}^{\mathsf {U}}$
and
$q^{\mathsf {U}} \in \mathbb {R}^{\mathsf {U}}$
and
![]() $u \in \mathbb {U}$
.
$u \in \mathbb {U}$
.
Lemma 3. Define the automorphism
i.e., we have
![]() $\chi = \psi ' \circ \varphi ' \circ \bar \chi \circ \varphi \circ \psi $
. Then,
$\chi = \psi ' \circ \varphi ' \circ \bar \chi \circ \varphi \circ \psi $
. Then,
![]() $\bar \chi |_{A_\alpha (\dot z)}=\text {id}$
for every
$\bar \chi |_{A_\alpha (\dot z)}=\text {id}$
for every
![]() $\alpha \in \kappa $
.
$\alpha \in \kappa $
.
Proof. Let
![]() $\alpha \in \kappa $
and
$\alpha \in \kappa $
and
![]() $q \in A_\alpha (\dot z)$
. We decompose
$q \in A_\alpha (\dot z)$
. We decompose
![]() $q=q^{\mathsf {R}} \oplus q^{\mathsf {U}} \oplus u$
as described above. From Fact 4 it follows that
$q=q^{\mathsf {R}} \oplus q^{\mathsf {U}} \oplus u$
as described above. From Fact 4 it follows that
![]() $\bar \chi (q)=\bar \chi (q^{\mathsf {R}}) \oplus \bar \chi (q^{\mathsf {U}}) \oplus \bar \chi (u)$
, and it therefore suffices to show that
$\bar \chi (q)=\bar \chi (q^{\mathsf {R}}) \oplus \bar \chi (q^{\mathsf {U}}) \oplus \bar \chi (u)$
, and it therefore suffices to show that
![]() $q^{\mathsf {R}}$
,
$q^{\mathsf {R}}$
,
![]() $q^{\mathsf {U}}$
and u are fixed by
$q^{\mathsf {U}}$
and u are fixed by
![]() $\bar \chi $
. We use Fact 3.
$\bar \chi $
. We use Fact 3.
Claim 1.
![]() $\bar \chi (q^{\mathsf {R}})=q^{\mathsf {R}}$
.
$\bar \chi (q^{\mathsf {R}})=q^{\mathsf {R}}$
.
Proof. This is clear, since all of
![]() $\psi , \varphi , \psi '$
and
$\psi , \varphi , \psi '$
and
![]() $\varphi '$
are the identity on
$\varphi '$
are the identity on
![]() $\mathbb {R}^{\mathsf {R}}$
, by (i).
$\mathbb {R}^{\mathsf {R}}$
, by (i).
Claim 2.
![]() $\bar \chi (q^{\mathsf {U}})=q^{\mathsf {U}}$
.
$\bar \chi (q^{\mathsf {U}})=q^{\mathsf {U}}$
.
Proof. Firstly,
![]() $\psi (q^{\mathsf {U}})= q^{\mathsf {U}} $
by (i). Next,
$\psi (q^{\mathsf {U}})= q^{\mathsf {U}} $
by (i). Next,
![]() $\varphi (q^{\mathsf {U}}) \in \mathbb {R}^\xi $
by (iv). Thus,
$\varphi (q^{\mathsf {U}}) \in \mathbb {R}^\xi $
by (iv). Thus,
![]() $\varphi (q^{\mathsf {U}})$
is fixed by the next two automorphisms
$\varphi (q^{\mathsf {U}})$
is fixed by the next two automorphisms
![]() $\psi '$
and then
$\psi '$
and then
![]() $\varphi '$
, by (i) and (vi), respectively. Then we again apply
$\varphi '$
, by (i) and (vi), respectively. Then we again apply
![]() $\varphi $
to get
$\varphi $
to get
![]() $\varphi (\varphi (q^{\mathsf {U}}))= q^{\mathsf {U}} $
. Finally,
$\varphi (\varphi (q^{\mathsf {U}}))= q^{\mathsf {U}} $
. Finally,
![]() $q^{\mathsf {U}} $
is fixed by
$q^{\mathsf {U}} $
is fixed by
![]() $\psi $
by (i).
$\psi $
by (i).
Claim 3.
![]() $\bar \chi (u)=u$
.
$\bar \chi (u)=u$
.
Proof. Firstly,
![]() $\psi (u) \in \mathbb {P}^\xi $
by (ii). Thus,
$\psi (u) \in \mathbb {P}^\xi $
by (ii). Thus,
![]() $\psi (u)$
is fixed by
$\psi (u)$
is fixed by
![]() $\varphi $
by (vii), by
$\varphi $
by (vii), by
![]() $\psi '$
by (v), by
$\psi '$
by (v), by
![]() $\varphi '$
by (vi) and then again by
$\varphi '$
by (vi) and then again by
![]() $\varphi $
by (vii). The final application of
$\varphi $
by (vii). The final application of
![]() $\psi $
gives
$\psi $
gives
![]() $\psi (\psi (u))=u$
.
$\psi (\psi (u))=u$
.
This finishes the proof of Lemma 3.
We are now ready to prove that
![]() $\chi $
does what we want it to do.
$\chi $
does what we want it to do.
Lemma 4. The automorphism
satisfies
![]() $\chi (\dot a_\xi )=\dot a_{\xi '}$
and
$\chi (\dot a_\xi )=\dot a_{\xi '}$
and
![]() $\chi (\dot a_{\xi '})=\dot a_{\xi }$
.
$\chi (\dot a_{\xi '})=\dot a_{\xi }$
.
Proof. We begin with the first equality. We have
![]() $\dot a_{\xi }=\bigcup _{\alpha \in \kappa } \{\check \alpha \}\times A_\alpha (\dot a_\xi )$
and thus,
$\dot a_{\xi }=\bigcup _{\alpha \in \kappa } \{\check \alpha \}\times A_\alpha (\dot a_\xi )$
and thus,
![]() $\chi (\dot a_\xi )= \bigcup _{\alpha \in \kappa } \{\check \alpha \}\times \chi [A_\alpha (\dot a_\xi )]$
. Therefore, we must show that for every
$\chi (\dot a_\xi )= \bigcup _{\alpha \in \kappa } \{\check \alpha \}\times \chi [A_\alpha (\dot a_\xi )]$
. Therefore, we must show that for every
![]() $\alpha \in \kappa : \chi [A_\alpha (\dot a_\xi )]=A_\alpha (\dot a_{\xi '})$
.
$\alpha \in \kappa : \chi [A_\alpha (\dot a_\xi )]=A_\alpha (\dot a_{\xi '})$
.
Let
![]() $\alpha \in \kappa $
. First, we deal with
$\alpha \in \kappa $
. First, we deal with
![]() $\chi [A_\alpha (\dot a_\xi )] \subseteq A_\alpha (\dot a_{\xi '})$
. Thus, let
$\chi [A_\alpha (\dot a_\xi )] \subseteq A_\alpha (\dot a_{\xi '})$
. Thus, let
![]() $p\in A_\alpha (\dot a_\xi )$
. We know that
$p\in A_\alpha (\dot a_\xi )$
. We know that
![]() $\varphi \circ \psi (\dot a_\xi )= \dot z$
, which implies that
$\varphi \circ \psi (\dot a_\xi )= \dot z$
, which implies that
![]() $q:=\varphi \circ \psi (p)\in A_\alpha (\dot z)$
. We also know that
$q:=\varphi \circ \psi (p)\in A_\alpha (\dot z)$
. We also know that
![]() $\psi ' \circ \varphi ' (\dot z)=\dot a_{\xi '}$
, and therefore
$\psi ' \circ \varphi ' (\dot z)=\dot a_{\xi '}$
, and therefore
![]() $\psi ' \circ \varphi ' (q) \in A_\alpha (\dot a_{\xi '})$
. Since
$\psi ' \circ \varphi ' (q) \in A_\alpha (\dot a_{\xi '})$
. Since
![]() $\bar \chi (q)=q$
by Lemma 3, we indeed obtain
$\bar \chi (q)=q$
by Lemma 3, we indeed obtain
The reverse inclusion
![]() $A_\alpha (\dot a_\xi ) \supseteq \chi ^{-1}[A_\alpha (\dot a_{\xi '})]$
follows from essentially the same proof: Note that
$A_\alpha (\dot a_\xi ) \supseteq \chi ^{-1}[A_\alpha (\dot a_{\xi '})]$
follows from essentially the same proof: Note that
![]() $\chi ^{-1}=\psi \circ \varphi \circ \bar \chi ^{-1} \circ \varphi ' \circ \psi '$
, and by Lemma 3,
$\chi ^{-1}=\psi \circ \varphi \circ \bar \chi ^{-1} \circ \varphi ' \circ \psi '$
, and by Lemma 3,
![]() $\bar \chi ^{-1}$
is the identity on
$\bar \chi ^{-1}$
is the identity on
![]() $A_\alpha (\dot z)$
as well.
$A_\alpha (\dot z)$
as well.
To show the second equality, i.e.,
![]() $\chi (\dot a_{\xi '})=\dot a_\xi $
, we again fix
$\chi (\dot a_{\xi '})=\dot a_\xi $
, we again fix
![]() $\alpha \in \kappa $
and show
$\alpha \in \kappa $
and show
![]() $\chi [A_\alpha (\dot a_{\xi '})]=A_\alpha (\dot a_\xi )$
. Here, we have to deal with the entire
$\chi [A_\alpha (\dot a_{\xi '})]=A_\alpha (\dot a_\xi )$
. Here, we have to deal with the entire
![]() $\chi $
at once, we again use Fact 3. To verify the direction “
$\chi $
at once, we again use Fact 3. To verify the direction “
![]() $\subseteq $
”, let
$\subseteq $
”, let
![]() $p' \in A_\alpha (\dot a_{\xi '})$
. Since
$p' \in A_\alpha (\dot a_{\xi '})$
. Since
![]() $p' \in \mathbb {S}^{\xi '}$
, we have
$p' \in \mathbb {S}^{\xi '}$
, we have
![]() $\psi (p')=p'$
by (v) and
$\psi (p')=p'$
by (v) and
![]() $\varphi (p')=p'$
by (vi). The next two automorphisms map
$\varphi (p')=p'$
by (vi). The next two automorphisms map
![]() $p'$
to
$p'$
to
![]() $\varphi '(\psi '(p'))$
, which is equal to a condition
$\varphi '(\psi '(p'))$
, which is equal to a condition
![]() $q \in A_\alpha (\dot z)$
, since
$q \in A_\alpha (\dot z)$
, since
![]() $\varphi '(\psi '(\dot a_{\xi '}))=\dot z$
. Then, q is mapped to
$\varphi '(\psi '(\dot a_{\xi '}))=\dot z$
. Then, q is mapped to
![]() $\psi (\varphi (q))$
, which is some
$\psi (\varphi (q))$
, which is some
![]() $p \in A_\alpha (\dot a_{\xi })$
, because
$p \in A_\alpha (\dot a_{\xi })$
, because
![]() $\psi (\varphi (\dot z))=\dot a_\xi $
. The last two automorphisms
$\psi (\varphi (\dot z))=\dot a_\xi $
. The last two automorphisms
![]() $\varphi '$
and
$\varphi '$
and
![]() $\psi '$
fix p, again by (v) and (vi).
$\psi '$
fix p, again by (v) and (vi).
Finally, the proof of the reverse inclusion
![]() $\chi [A_\alpha (\dot a_{\xi '})] \supseteq A_\alpha (\dot a_\xi )$
is analogous and left as an exercise to the reader.
$\chi [A_\alpha (\dot a_{\xi '})] \supseteq A_\alpha (\dot a_\xi )$
is analogous and left as an exercise to the reader.
3. Globally large tower spectra
Next, we show that arbitrarily large tower spectra at all regular cardinals simultaneously are consistent. In fact, we show that
![]() $\mathfrak {sp}(\mathfrak {t}_{\text {cl}}(\kappa ))$
can be arbitrarily large globally. The forcing notion we use is similar to a part of the forcing notion developed by Hechler in [Reference Hechler7], designed to force the existence of many
$\mathfrak {sp}(\mathfrak {t}_{\text {cl}}(\kappa ))$
can be arbitrarily large globally. The forcing notion we use is similar to a part of the forcing notion developed by Hechler in [Reference Hechler7], designed to force the existence of many
![]() $\omega $
-towers.
$\omega $
-towers.
Theorem 3. Let
![]() $\mathbf {V}\models \mathsf {GCH}$
and let E be an Easton function. There is a forcing extension of
$\mathbf {V}\models \mathsf {GCH}$
and let E be an Easton function. There is a forcing extension of
![]() $\mathbf {V}$
in which
$\mathbf {V}$
in which
Proof. We begin by defining the relevant forcing notion.
Definition 11. Define for each
![]() $\kappa \in \text {dom}(E)$
the set
$\kappa \in \text {dom}(E)$
the set
![]() $\mathcal {I}^{\kappa }:=\{\langle \kappa , \xi \rangle : \xi \in E(\kappa )\}$
, which serves as an index set. The purpose of the entry
$\mathcal {I}^{\kappa }:=\{\langle \kappa , \xi \rangle : \xi \in E(\kappa )\}$
, which serves as an index set. The purpose of the entry
![]() $\kappa $
is to ensure that the different
$\kappa $
is to ensure that the different
![]() $\mathcal {I}^{\kappa }$
are disjoint.
$\mathcal {I}^{\kappa }$
are disjoint.
For each
![]() $\kappa \in \text {dom}(E)$
, let
$\kappa \in \text {dom}(E)$
, let
![]() $\mathbb {T}^{\kappa }$
consist of conditions
$\mathbb {T}^{\kappa }$
consist of conditions
![]() $q: \Delta ^{q} \times \eta ^{q} \to 2$
, where
$q: \Delta ^{q} \times \eta ^{q} \to 2$
, where
![]() ${\Delta ^{q} \in [\mathcal {I}^{\kappa }]^{{<}\kappa }}$
and
${\Delta ^{q} \in [\mathcal {I}^{\kappa }]^{{<}\kappa }}$
and
![]() $\eta ^{q} \in \kappa \setminus \{0\}$
. Let
$\eta ^{q} \in \kappa \setminus \{0\}$
. Let
![]() $q' \leq q$
iff
$q' \leq q$
iff
-
(i)
 $q \subseteq q' $
,
$q \subseteq q' $
, -
(ii) For all
 $\xi < \xi ' \text { with } \langle \kappa , \xi \rangle , \langle \kappa , \xi '\rangle \in \Delta ^{q}$
and for all
$\xi < \xi ' \text { with } \langle \kappa , \xi \rangle , \langle \kappa , \xi '\rangle \in \Delta ^{q}$
and for all
 $\eta ^{q}\leq \mu < \eta ^{q'}: q'(\langle \kappa , \xi \rangle , \mu )=0 \implies q'(\langle \kappa , \xi ' \rangle , \mu )=0$
.
$\eta ^{q}\leq \mu < \eta ^{q'}: q'(\langle \kappa , \xi \rangle , \mu )=0 \implies q'(\langle \kappa , \xi ' \rangle , \mu )=0$
.
Let
![]() $\mathbb {T}$
be the Easton-product of the
$\mathbb {T}$
be the Easton-product of the
![]() $\mathbb {T}^\kappa $
.
$\mathbb {T}^\kappa $
.
Lemma 5. Let
![]() $\kappa \in \text {dom}(E)$
and decompose
$\kappa \in \text {dom}(E)$
and decompose
![]() $\mathbb {T}$
as
$\mathbb {T}$
as
![]() $\mathbb {T}^{\leq \kappa } \times \mathbb {T}^{{>}\kappa }$
. Then,
$\mathbb {T}^{\leq \kappa } \times \mathbb {T}^{{>}\kappa }$
. Then,
![]() $\mathbb {T}^{{>}\kappa } $
is
$\mathbb {T}^{{>}\kappa } $
is
![]() $\kappa ^{+}$
-closed and
$\kappa ^{+}$
-closed and
![]() $\mathbb {T}^{\leq \kappa }$
satisfies the
$\mathbb {T}^{\leq \kappa }$
satisfies the
![]() $\kappa ^{+}$
-c.c.
$\kappa ^{+}$
-c.c.
Proof. The first statement is easy to verify. To show the second statement, let A be a
![]() $\kappa ^{+}$
-sized set of
$\kappa ^{+}$
-sized set of
![]() $\mathbb {T}^{\leq \kappa }$
-conditions. For each
$\mathbb {T}^{\leq \kappa }$
-conditions. For each
![]() $p\in A$
, let
$p\in A$
, let
![]() $S_p:=\bigcup \{\Delta ^{p(\delta )}\times \eta ^{p(\delta )}: \delta \in \text {supp}(p)\}$
. Note that
$S_p:=\bigcup \{\Delta ^{p(\delta )}\times \eta ^{p(\delta )}: \delta \in \text {supp}(p)\}$
. Note that
![]() $S_p$
has cardinality
$S_p$
has cardinality
![]() ${<}\kappa $
. By the
${<}\kappa $
. By the
![]() $\Delta $
-system Lemma, we obtain some
$\Delta $
-system Lemma, we obtain some
![]() $A'\subseteq A$
of cardinality
$A'\subseteq A$
of cardinality
![]() $\kappa ^{+}$
and for each
$\kappa ^{+}$
and for each
![]() $\delta \in \text {dom}(E^{\leq \kappa })$
some
$\delta \in \text {dom}(E^{\leq \kappa })$
some
![]() $R^{\delta }\in [\mathcal {I}^{\delta }]^{{<}\delta }$
and some
$R^{\delta }\in [\mathcal {I}^{\delta }]^{{<}\delta }$
and some
![]() $r^{\delta } \in \delta $
, such that for all these
$r^{\delta } \in \delta $
, such that for all these
![]() $\delta $
and all
$\delta $
and all
![]() $p \neq p' \in A': (\Delta ^{p(\delta )}\times \eta ^{p(\delta )}) \cap (\Delta ^{p'(\delta )}\times \eta ^{p'(\delta )})= R^{\delta } \times r^{\delta } $
. Note that the set
$p \neq p' \in A': (\Delta ^{p(\delta )}\times \eta ^{p(\delta )}) \cap (\Delta ^{p'(\delta )}\times \eta ^{p'(\delta )})= R^{\delta } \times r^{\delta } $
. Note that the set
![]() $C:=\{\delta : R^{\delta } \times r^{\delta } \neq \emptyset \}$
has cardinality
$C:=\{\delta : R^{\delta } \times r^{\delta } \neq \emptyset \}$
has cardinality
![]() ${<}\kappa $
. For each
${<}\kappa $
. For each
![]() $\delta \in C$
, there is at most one
$\delta \in C$
, there is at most one
![]() $p\in A'$
with
$p\in A'$
with
![]() $\eta ^{p(\delta )}\neq r^{\delta }$
. By removing these
$\eta ^{p(\delta )}\neq r^{\delta }$
. By removing these
![]() ${<}\kappa $
many conditions, we can assume that no such p exist in
${<}\kappa $
many conditions, we can assume that no such p exist in
![]() $A'$
.
$A'$
.
The set
![]() $\bigcup \{R^{\delta } \times r^{\delta }: \delta \in C \}$
has cardinality
$\bigcup \{R^{\delta } \times r^{\delta }: \delta \in C \}$
has cardinality
![]() ${<}\kappa $
. By the
${<}\kappa $
. By the
![]() $\mathsf {GCH}$
, we have
$\mathsf {GCH}$
, we have
![]() $2^{{<}\kappa }=\kappa $
, and we can therefore assume that for all
$2^{{<}\kappa }=\kappa $
, and we can therefore assume that for all
![]() $p,p' \in A'$
and all
$p,p' \in A'$
and all
![]() $\delta \in \text {dom}(E^{\leq \kappa })$
, the functions
$\delta \in \text {dom}(E^{\leq \kappa })$
, the functions
![]() $p(\delta )$
and
$p(\delta )$
and
![]() $p'(\delta )$
agree on the intersection of their domains. It is now easy to verify that the conditions in
$p'(\delta )$
agree on the intersection of their domains. It is now easy to verify that the conditions in
![]() $A'$
are pairwise compatible.
$A'$
are pairwise compatible.
It follows by standard methods that
Corollary 2.
![]() $\mathbb {T}$
preserves cofinalities and hence cardinals.
$\mathbb {T}$
preserves cofinalities and hence cardinals.
See, for example, the proof of Easton’s Theorem in [Reference Kunen9, Chapter VIII and Lemma 4.6].
Proposition 1. Let
![]() $\mathbf {V}\models \textrm {GCH}$
and let G be
$\mathbf {V}\models \textrm {GCH}$
and let G be
![]() $\mathbb {T}$
-generic over
$\mathbb {T}$
-generic over
![]() $\mathbf {V}$
. Then, for any
$\mathbf {V}$
. Then, for any
![]() ${\kappa \in \text {dom}(E)}$
and any regular
${\kappa \in \text {dom}(E)}$
and any regular
![]() $\lambda \in [\kappa ^{+}, E(\kappa )]$
, there is a
$\lambda \in [\kappa ^{+}, E(\kappa )]$
, there is a
![]() $\kappa $
-tower of length
$\kappa $
-tower of length
![]() $\lambda $
consisting of clubs in
$\lambda $
consisting of clubs in
![]() $\mathbf {V}[G]$
.
$\mathbf {V}[G]$
.
Proof. Let
![]() $\kappa \in \text {dom}(E)$
and
$\kappa \in \text {dom}(E)$
and
![]() $\lambda \in [\kappa ^{+}, E(\kappa )]$
. As before, decompose
$\lambda \in [\kappa ^{+}, E(\kappa )]$
. As before, decompose
![]() $\mathbb {T}$
as
$\mathbb {T}$
as
![]() $\mathbb {T}^{\leq \kappa } \times \mathbb {T}^{{>}\kappa }$
and
$\mathbb {T}^{\leq \kappa } \times \mathbb {T}^{{>}\kappa }$
and
![]() $G=G^{\leq \kappa }\times G^{{>}\kappa }$
accordingly. Since
$G=G^{\leq \kappa }\times G^{{>}\kappa }$
accordingly. Since
![]() $\mathbb {T}^{{>}\kappa }$
is
$\mathbb {T}^{{>}\kappa }$
is
![]() $\kappa ^{+}$
-closed, the
$\kappa ^{+}$
-closed, the
![]() $\mathsf {GCH}$
at
$\mathsf {GCH}$
at
![]() $\delta \leq \kappa $
still holds in
$\delta \leq \kappa $
still holds in
![]() $\mathbf {V}[G ^{> \kappa }]$
and
$\mathbf {V}[G ^{> \kappa }]$
and
![]() $(\mathbb {T}^{\leq \kappa })^{\mathbf {V}[G ^{> \kappa }]}=(\mathbb {T}^{\leq \kappa })^{\mathbf {V}}$
. We work in
$(\mathbb {T}^{\leq \kappa })^{\mathbf {V}[G ^{> \kappa }]}=(\mathbb {T}^{\leq \kappa })^{\mathbf {V}}$
. We work in
![]() $\mathbf {W}:=\mathbf {V}[G ^{> \kappa }]$
.
$\mathbf {W}:=\mathbf {V}[G ^{> \kappa }]$
.
Since
![]() $\kappa $
and
$\kappa $
and
![]() $\lambda $
are fixed and since we are only interested in the
$\lambda $
are fixed and since we are only interested in the
![]() $\kappa $
-th coordinate of each
$\kappa $
-th coordinate of each
![]() $\mathbb {T}^{\leq \kappa }$
-condition p, define for notational simplicity for each
$\mathbb {T}^{\leq \kappa }$
-condition p, define for notational simplicity for each
![]() $p \in \mathbb {T}^{\leq \kappa } $
the following abbreviation
$p \in \mathbb {T}^{\leq \kappa } $
the following abbreviation
![]() $q_p$
:
$q_p$
:
-
(i)
 $\forall \xi \in E(\kappa )\;\forall \alpha \in \kappa : q_p(\xi , \alpha ):=p(\kappa )(\langle \kappa , \xi \rangle , \alpha ).$
$\forall \xi \in E(\kappa )\;\forall \alpha \in \kappa : q_p(\xi , \alpha ):=p(\kappa )(\langle \kappa , \xi \rangle , \alpha ).$
-
(ii)
 $\Delta ^{q_p}:= \Delta ^{p(\kappa )}.$
$\Delta ^{q_p}:= \Delta ^{p(\kappa )}.$
-
(iii)
 $\eta ^{q_p}:=\eta ^{p(\kappa )}$
.
$\eta ^{q_p}:=\eta ^{p(\kappa )}$
.
In
![]() $\mathbf {W}[G^{\leq \kappa }]$
, define for each
$\mathbf {W}[G^{\leq \kappa }]$
, define for each
![]() $\xi \in E(\kappa )$
the
$\xi \in E(\kappa )$
the
![]() $\kappa $
-real
$\kappa $
-real
![]() $g_\xi := \{\alpha \in \kappa : \exists p \in G^{\leq \kappa }: q_p(\xi , \alpha ) =1\}$
. We assume that
$g_\xi := \{\alpha \in \kappa : \exists p \in G^{\leq \kappa }: q_p(\xi , \alpha ) =1\}$
. We assume that
![]() $\lambda < E(\kappa )$
and define
$\lambda < E(\kappa )$
and define
![]() $a_\xi :=\text {cl}(g_\xi \setminus g_\lambda )$
for all
$a_\xi :=\text {cl}(g_\xi \setminus g_\lambda )$
for all
![]() $\xi < \lambda $
. We show that the sequence
$\xi < \lambda $
. We show that the sequence
![]() $\langle a_{\xi }: \xi \in \lambda \rangle $
is a
$\langle a_{\xi }: \xi \in \lambda \rangle $
is a
![]() $\kappa $
-tower of length
$\kappa $
-tower of length
![]() $\lambda $
in
$\lambda $
in
![]() $\mathbf {W}[G^{\leq \kappa }]$
. If
$\mathbf {W}[G^{\leq \kappa }]$
. If
![]() $\lambda = E(\kappa )$
, it follows by a very similar but simplified argument that setting
$\lambda = E(\kappa )$
, it follows by a very similar but simplified argument that setting
![]() $a_\xi := \text {cl}(g_\xi )$
yields a
$a_\xi := \text {cl}(g_\xi )$
yields a
![]() $\kappa $
-tower of length
$\kappa $
-tower of length
![]() $E(\kappa )$
.
$E(\kappa )$
.
It is easy to see that
![]() $\langle g_{\xi }: \xi \in E(\kappa )\rangle $
is well-ordered by
$\langle g_{\xi }: \xi \in E(\kappa )\rangle $
is well-ordered by
![]() $\supseteq ^{*}$
, and therefore,
$\supseteq ^{*}$
, and therefore,
![]() $\langle a_{\xi }: \xi \in \lambda \rangle $
is as well. In order to show that
$\langle a_{\xi }: \xi \in \lambda \rangle $
is as well. In order to show that
![]() $\langle a_{\xi }: \xi \in \lambda \rangle $
does not have a pseudo-intersection in
$\langle a_{\xi }: \xi \in \lambda \rangle $
does not have a pseudo-intersection in
![]() $\mathbf {W}[G^{\leq \kappa }]$
, let
$\mathbf {W}[G^{\leq \kappa }]$
, let
![]() $\dot x$
be a
$\dot x$
be a
![]() $\mathbb {T}^{\leq \kappa }$
-name for a subset of
$\mathbb {T}^{\leq \kappa }$
-name for a subset of
![]() $\kappa $
and
$\kappa $
and
![]() $p_0 \in G^{\leq \kappa }$
a condition such that
$p_0 \in G^{\leq \kappa }$
a condition such that
![]() $p_0 \Vdash {"}|\dot x|=\kappa "$
. For each
$p_0 \Vdash {"}|\dot x|=\kappa "$
. For each
![]() $\alpha \in \kappa $
, let
$\alpha \in \kappa $
, let
![]() $A_{\alpha }$
be a maximal antichain deciding
$A_{\alpha }$
be a maximal antichain deciding
![]() $"\alpha \in \dot x"$
. By the
$"\alpha \in \dot x"$
. By the
![]() $\kappa ^{+}$
-c.c. of
$\kappa ^{+}$
-c.c. of
![]() $\mathbb {T}^{\leq \kappa }$
, the set
$\mathbb {T}^{\leq \kappa }$
, the set
![]() $\Delta := \bigcup \{\Delta ^{q_p}: p \in A_\alpha ,\;\alpha \in \kappa \}$
has cardinality at most
$\Delta := \bigcup \{\Delta ^{q_p}: p \in A_\alpha ,\;\alpha \in \kappa \}$
has cardinality at most
![]() $\kappa $
. Thus, by regularity of
$\kappa $
. Thus, by regularity of
![]() $\lambda $
, there exists
$\lambda $
, there exists
![]() $\langle \kappa , \xi _0\rangle \in \mathcal {I}^{\kappa }$
such that
$\langle \kappa , \xi _0\rangle \in \mathcal {I}^{\kappa }$
such that
![]() $\xi < \xi _0 < \lambda $
for every
$\xi < \xi _0 < \lambda $
for every
![]() $\xi < \lambda $
with
$\xi < \lambda $
with
![]() $\langle \kappa , \xi \rangle \in \Delta $
. We show that for every
$\langle \kappa , \xi \rangle \in \Delta $
. We show that for every
![]() $\nu \in \kappa $
, the set of conditions forcing
$\nu \in \kappa $
, the set of conditions forcing
![]() $"\dot x \setminus \nu \nsubseteq \dot {a}_{\xi _0}"$
is dense below
$"\dot x \setminus \nu \nsubseteq \dot {a}_{\xi _0}"$
is dense below
![]() $p_0$
.
$p_0$
.
Let
![]() $p \leq p_0$
. By extending p, we can assume that
$p \leq p_0$
. By extending p, we can assume that
![]() $\langle \kappa , \lambda \rangle \in \Delta ^{q_p}$
. Since
$\langle \kappa , \lambda \rangle \in \Delta ^{q_p}$
. Since
![]() $p \Vdash {"}|\dot x|=\kappa " $
, there exists
$p \Vdash {"}|\dot x|=\kappa " $
, there exists
![]() $\alpha _0> \max \{\eta ^{q_p}, \nu \}$
and
$\alpha _0> \max \{\eta ^{q_p}, \nu \}$
and
![]() $\bar p \leq p$
with
$\bar p \leq p$
with
![]() $\bar p \Vdash \check \alpha _0 \in \dot x$
. Therefore
$\bar p \Vdash \check \alpha _0 \in \dot x$
. Therefore
![]() $\bar p$
is compatible with some
$\bar p$
is compatible with some
![]() $r \in A_{\alpha _0}$
via some common extension s. In particular, p and r are compatible via s. Without loss of generality, we can assume that
$r \in A_{\alpha _0}$
via some common extension s. In particular, p and r are compatible via s. Without loss of generality, we can assume that
![]() $\langle \xi _0, \alpha _0 \rangle , \langle \lambda , \alpha _0\rangle \in \text {dom}(q_s)$
.
$\langle \xi _0, \alpha _0 \rangle , \langle \lambda , \alpha _0\rangle \in \text {dom}(q_s)$
.
Note that for all
![]() $\xi _0 \leq \xi < \lambda $
and all
$\xi _0 \leq \xi < \lambda $
and all
![]() $\max \{\eta ^{q_p}, \nu \}\leq \alpha \leq \alpha _0$
with
$\max \{\eta ^{q_p}, \nu \}\leq \alpha \leq \alpha _0$
with
![]() $\langle \xi , \alpha \rangle \in \text {dom}(q_{s}):\langle \xi , \alpha \rangle \notin \text {dom}(q_p) \cup \text {dom}(q_r)$
, since
$\langle \xi , \alpha \rangle \in \text {dom}(q_{s}):\langle \xi , \alpha \rangle \notin \text {dom}(q_p) \cup \text {dom}(q_r)$
, since
![]() $\alpha \geq \eta ^{q_p}$
and by the choice of
$\alpha \geq \eta ^{q_p}$
and by the choice of
![]() $\xi _0$
. Therefore, we can set
$\xi _0$
. Therefore, we can set
![]() $\bar s$
equal to s except that for all such
$\bar s$
equal to s except that for all such
![]() $\xi $
and
$\xi $
and
![]() $\alpha : q_{\bar s}(\xi , \alpha ):=\min \{q_s(\xi , \alpha ),\,q_s(\lambda , \alpha )\}$
. It follows that
$\alpha : q_{\bar s}(\xi , \alpha ):=\min \{q_s(\xi , \alpha ),\,q_s(\lambda , \alpha )\}$
. It follows that
![]() $\bar s$
is a common extension of p and r, and for every
$\bar s$
is a common extension of p and r, and for every
![]() $\max \{\eta ^{q_p}, \nu \}\leq \alpha \leq \alpha _0: \;\bar s \Vdash {"}\check \alpha \in \dot g_{\xi _0} \implies \check \alpha \in \dot g_{\lambda }"$
. Thus,
$\max \{\eta ^{q_p}, \nu \}\leq \alpha \leq \alpha _0: \;\bar s \Vdash {"}\check \alpha \in \dot g_{\xi _0} \implies \check \alpha \in \dot g_{\lambda }"$
. Thus,
![]() $\bar s \Vdash {"}\check \alpha _0 \in \dot x \setminus \text {cl}(\dot g_{\xi _0}\setminus \dot g_{\lambda })"$
, finishing the proof of the proposition.
$\bar s \Vdash {"}\check \alpha _0 \in \dot x \setminus \text {cl}(\dot g_{\xi _0}\setminus \dot g_{\lambda })"$
, finishing the proof of the proposition.
Lastly, it can be checked easily, by counting nice
![]() $\mathbb {T}^{\leq \kappa }$
-names for subsets of
$\mathbb {T}^{\leq \kappa }$
-names for subsets of
![]() $\kappa $
, that
$\kappa $
, that
![]() $\forall \kappa \in \text {dom}(E): 2^\kappa =E(\kappa )$
in every
$\forall \kappa \in \text {dom}(E): 2^\kappa =E(\kappa )$
in every
![]() $\mathbb {T}$
-generic extension of
$\mathbb {T}$
-generic extension of
![]() $\mathbf {V}\models \mathsf {GCH}$
.
$\mathbf {V}\models \mathsf {GCH}$
.
Corollary 3. In the above extension,
![]() $\mathfrak {b}(\kappa )=\kappa ^{+}$
for every
$\mathfrak {b}(\kappa )=\kappa ^{+}$
for every
![]() $\kappa \in \text {dom}(E)$
.
$\kappa \in \text {dom}(E)$
.
Proof. For uncountable
![]() $\kappa $
, this follows from Lemma 1. In the case
$\kappa $
, this follows from Lemma 1. In the case
![]() $\kappa =\omega $
, it can easily be seen that the forcing notion
$\kappa =\omega $
, it can easily be seen that the forcing notion
![]() $\mathbb {T}^{\omega }$
densely embeds into the part of the forcing notion introduced by Hechler [Reference Hechler7] that deals with towers. The first author, Koelbing and Wohofsky [Reference Fischer, Koelbing and Wohofsky6, Corollary 5.1] have shown that the latter forces
$\mathbb {T}^{\omega }$
densely embeds into the part of the forcing notion introduced by Hechler [Reference Hechler7] that deals with towers. The first author, Koelbing and Wohofsky [Reference Fischer, Koelbing and Wohofsky6, Corollary 5.1] have shown that the latter forces
![]() $\mathfrak {b}(\omega )=\omega _1$
, by showing that it decomposes as a finite support iteration of Mathias forcings that preserve the unboundedness of ground model scales.
$\mathfrak {b}(\omega )=\omega _1$
, by showing that it decomposes as a finite support iteration of Mathias forcings that preserve the unboundedness of ground model scales.
4. A locally bounded tower spectrum
Our final result establishes that the
![]() $\kappa $
-tower spectrum may consistently have any upper bound below
$\kappa $
-tower spectrum may consistently have any upper bound below
![]() $2^\kappa $
, where this upper bound is given by
$2^\kappa $
, where this upper bound is given by
![]() $\mathfrak {b}(\kappa )$
.
$\mathfrak {b}(\kappa )$
.
Theorem 4. Assume
![]() $\mathbf {V}\models \mathsf {GCH}$
. Let
$\mathbf {V}\models \mathsf {GCH}$
. Let
![]() $\kappa < \beta $
be regular and let
$\kappa < \beta $
be regular and let
![]() $\mu $
be such that
$\mu $
be such that
![]() ${\text {cf}(\mu )\geq \beta }$
. There is a generic extension of
${\text {cf}(\mu )\geq \beta }$
. There is a generic extension of
![]() $\mathbf {V}$
in which
$\mathbf {V}$
in which
Proof. We begin by briefly sketching the idea of the proof. We force
![]() $\mathfrak {b}(\kappa )=\beta $
and
$\mathfrak {b}(\kappa )=\beta $
and
![]() $2^\kappa =\mu $
using a non-linear iteration of
$2^\kappa =\mu $
using a non-linear iteration of
![]() $\kappa $
-Hechler forcing. Non-linear iterations of Hechler forcing at
$\kappa $
-Hechler forcing. Non-linear iterations of Hechler forcing at
![]() $\omega $
were introduced by Hechler in [Reference Hechler8] and generalized to the uncountable by Cummings and Shelah in [Reference Cummings and Shelah3]. The strategy is to force the existence of a cofinal embedding from some partial order
$\omega $
were introduced by Hechler in [Reference Hechler8] and generalized to the uncountable by Cummings and Shelah in [Reference Cummings and Shelah3]. The strategy is to force the existence of a cofinal embedding from some partial order
![]() $\mathbb {Q}$
into the partial order
$\mathbb {Q}$
into the partial order
![]() $(\kappa ^\kappa , \leq ^{*})$
, where an order-preserving embedding
$(\kappa ^\kappa , \leq ^{*})$
, where an order-preserving embedding
![]() $f: \mathbb {Q} \to \mathbb {Q}'$
is cofinal iff
$f: \mathbb {Q} \to \mathbb {Q}'$
is cofinal iff
![]() $\forall p \in \mathbb {Q}'\; \exists q \in \mathbb {Q}: p \leq _{\mathbb {Q}'}f(q)$
. By choosing a
$\forall p \in \mathbb {Q}'\; \exists q \in \mathbb {Q}: p \leq _{\mathbb {Q}'}f(q)$
. By choosing a
![]() $\mathbb {Q}$
with appropriate bounding and dominating properties, one obtains the desired values of
$\mathbb {Q}$
with appropriate bounding and dominating properties, one obtains the desired values of
![]() $\mathfrak {b}(\kappa )$
and
$\mathfrak {b}(\kappa )$
and
![]() $\mathfrak {d}(\kappa )$
in the extension. These properties are formalized by the following definition.
$\mathfrak {d}(\kappa )$
in the extension. These properties are formalized by the following definition.
Definition 12. Let
![]() $\mathbb {Q}$
be a partially ordered set. We say that
$\mathbb {Q}$
be a partially ordered set. We say that
![]() $B \subseteq \mathbb {Q}$
is unbounded iff
$B \subseteq \mathbb {Q}$
is unbounded iff
![]() $\forall q \in \mathbb {Q}\;\exists p \in B: p \nleq _{\mathbb {Q}}q$
. Let
$\forall q \in \mathbb {Q}\;\exists p \in B: p \nleq _{\mathbb {Q}}q$
. Let
![]() $\mathfrak {b}(\mathbb {Q})$
be the minimal cardinality of an unbounded subset of
$\mathfrak {b}(\mathbb {Q})$
be the minimal cardinality of an unbounded subset of
![]() $\mathbb {Q}$
and let
$\mathbb {Q}$
and let
![]() $\mathfrak {d}(\mathbb {Q})$
be the minimal cardinality of a cofinal (or dominating) subset of
$\mathfrak {d}(\mathbb {Q})$
be the minimal cardinality of a cofinal (or dominating) subset of
![]() $\mathbb {Q}$
. Thus,
$\mathbb {Q}$
. Thus,
![]() $\mathfrak {b}(\kappa )=\mathfrak {b}((\kappa ^\kappa , \leq ^{*}))$
and
$\mathfrak {b}(\kappa )=\mathfrak {b}((\kappa ^\kappa , \leq ^{*}))$
and
![]() $\mathfrak {d}(\kappa )=\mathfrak {d}((\kappa ^\kappa , \leq ^{*}))$
.
$\mathfrak {d}(\kappa )=\mathfrak {d}((\kappa ^\kappa , \leq ^{*}))$
.
The following fact is easy to check.
Fact 5. If
![]() $f: \mathbb {Q} \to \mathbb {Q}'$
is a cofinal embedding, then
$f: \mathbb {Q} \to \mathbb {Q}'$
is a cofinal embedding, then
![]() $\mathfrak {b}(\mathbb {Q}')=\mathfrak {b}(\mathbb {Q})$
and
$\mathfrak {b}(\mathbb {Q}')=\mathfrak {b}(\mathbb {Q})$
and
![]() $\mathfrak {d}(\mathbb {Q}')=\mathfrak {d}(\mathbb {Q})$
.
$\mathfrak {d}(\mathbb {Q}')=\mathfrak {d}(\mathbb {Q})$
.
Therefore, by choosing a
![]() $\mathbb {Q}$
satisfying
$\mathbb {Q}$
satisfying
![]() $\mathfrak {b}(\mathbb {Q})=\beta $
and
$\mathfrak {b}(\mathbb {Q})=\beta $
and
![]() $\mathfrak {d}(\mathbb {Q})=\mu $
in the forcing extension, we will obtain
$\mathfrak {d}(\mathbb {Q})=\mu $
in the forcing extension, we will obtain
![]() $\mathfrak {b}(\kappa )=\beta $
and
$\mathfrak {b}(\kappa )=\beta $
and
![]() $2^\kappa \geq \mathfrak {d}(\kappa )=\mu $
. The reverse inequality
$2^\kappa \geq \mathfrak {d}(\kappa )=\mu $
. The reverse inequality
![]() ${2^\kappa \leq \mu }$
will follow by counting nice names.
${2^\kappa \leq \mu }$
will follow by counting nice names.
We then show that there are no
![]() $\kappa $
-towers of length greater than
$\kappa $
-towers of length greater than
![]() $\beta $
in the forcing extension, again due to an isomorphism of names. For this argument to succeed, we first use a preparatory forcing to obtain a particular partial order, one in which every element only lies above few others. This complication stems from the fact that we need to iterate along a well-founded partial order, where
$\beta $
in the forcing extension, again due to an isomorphism of names. For this argument to succeed, we first use a preparatory forcing to obtain a particular partial order, one in which every element only lies above few others. This complication stems from the fact that we need to iterate along a well-founded partial order, where
![]() $\mathbb {Q}$
is well-founded if every
$\mathbb {Q}$
is well-founded if every
![]() $C \subseteq \mathbb {Q}$
contains a minimal element. While it is folklore that every partial order contains a cofinal, well-founded subset, choosing any such subset in our proof will not yield the upper bound we aim for. Note however that the preparatory forcing step could be skipped if we were to start with an inaccessible
$C \subseteq \mathbb {Q}$
contains a minimal element. While it is folklore that every partial order contains a cofinal, well-founded subset, choosing any such subset in our proof will not yield the upper bound we aim for. Note however that the preparatory forcing step could be skipped if we were to start with an inaccessible
![]() $\beta $
.
$\beta $
.
Lemma 6. Assume
![]() $\beta $
is regular,
$\beta $
is regular,
![]() $\beta ^{{<}\beta }=\beta $
and
$\beta ^{{<}\beta }=\beta $
and
![]() $\mu $
is such that
$\mu $
is such that
![]() $\text {cf}(\mu )\geq \beta $
. Consider the partial order
$\text {cf}(\mu )\geq \beta $
. Consider the partial order
![]() $([\mu ]^{<\beta }, \subseteq )$
. There is a
$([\mu ]^{<\beta }, \subseteq )$
. There is a
![]() $\beta $
-closed,
$\beta $
-closed,
![]() $\beta ^{+}$
-c.c. forcing notion
$\beta ^{+}$
-c.c. forcing notion
![]() $\mathbb {P}$
that adds a cofinal subset
$\mathbb {P}$
that adds a cofinal subset
![]() $\mathbb {Q}^{*}\subseteq [\mu ]^{{<}\beta }$
, satisfying:
$\mathbb {Q}^{*}\subseteq [\mu ]^{{<}\beta }$
, satisfying:
-
(i)
 $\mathbb {Q}^{*}$
is well-founded,
$\mathbb {Q}^{*}$
is well-founded, -
(ii) For all
 $x \in \mathbb {Q}^{*}: |\{y \in \mathbb {Q}^{*}: y \subseteq x\}| < \beta $
,
$x \in \mathbb {Q}^{*}: |\{y \in \mathbb {Q}^{*}: y \subseteq x\}| < \beta $
, -
(iii)
 $\mathfrak {b}(\mathbb {Q}^{*})=\beta $
,
$\mathfrak {b}(\mathbb {Q}^{*})=\beta $
, -
(iv)
 $\mathfrak {d}(\mathbb {Q}^{*})=|\mathbb {Q}^{*}|=\mu $
.
$\mathfrak {d}(\mathbb {Q}^{*})=|\mathbb {Q}^{*}|=\mu $
.
Proof. Let p be a
![]() $\mathbb {P}$
-condition iff p is a well-founded subset of
$\mathbb {P}$
-condition iff p is a well-founded subset of
![]() $[\mu ]^{{<}\beta }$
of cardinality
$[\mu ]^{{<}\beta }$
of cardinality
![]() ${<}\beta $
. The order is given by
${<}\beta $
. The order is given by
Claim 4.
![]() $\mathbb {P}$
is
$\mathbb {P}$
is
![]() $\beta $
-closed and satisfies the
$\beta $
-closed and satisfies the
![]() $\beta ^{+}$
-c.c.
$\beta ^{+}$
-c.c.
Proof. Checking the first part is routine. For the second part, let
![]() $A\in [\mathbb {P}]^{\beta ^{+}}$
. Applying the
$A\in [\mathbb {P}]^{\beta ^{+}}$
. Applying the
![]() $\Delta $
-system Lemma to the family
$\Delta $
-system Lemma to the family
![]() $\{\bigcup p: p \in A\}$
yields some
$\{\bigcup p: p \in A\}$
yields some
![]() $A' \subseteq A$
of cardinality
$A' \subseteq A$
of cardinality
![]() $\beta ^{+}$
and a root
$\beta ^{+}$
and a root
![]() $R \in [\mu ]^{{<}\beta }$
. There are at most
$R \in [\mu ]^{{<}\beta }$
. There are at most
![]() $2^{{<}\beta }=\beta $
many subsets of R, and since
$2^{{<}\beta }=\beta $
many subsets of R, and since
![]() $\beta ^{{<}\beta }=\beta $
, we can assume that
$\beta ^{{<}\beta }=\beta $
, we can assume that
![]() $p \cap \mathcal {P}(R)$
does not depend on
$p \cap \mathcal {P}(R)$
does not depend on
![]() $p \in A'$
. It follows that the
$p \in A'$
. It follows that the
![]() $p \in A'$
are pairwise compatible.
$p \in A'$
are pairwise compatible.
Now, let H be
![]() $\mathbb {P}$
-generic over
$\mathbb {P}$
-generic over
![]() $\mathbf {V}$
and define
$\mathbf {V}$
and define
![]() $\mathbb {Q}^{*}:=\bigcup H$
. By the above claim, cardinalities and cofinalities are preserved in
$\mathbb {Q}^{*}:=\bigcup H$
. By the above claim, cardinalities and cofinalities are preserved in
![]() $\mathbf {V}[H]$
and we have
$\mathbf {V}[H]$
and we have
![]() $([\mu ]^{<\beta })^{\mathbf {V}[H]}=([\mu ]^{<\beta })^{\mathbf {V}}$
.
$([\mu ]^{<\beta })^{\mathbf {V}[H]}=([\mu ]^{<\beta })^{\mathbf {V}}$
.
It is easy to see that for every
![]() $x \in [\mu ]^{{<}\beta }$
, the set
$x \in [\mu ]^{{<}\beta }$
, the set
![]() $\mathcal {D}_x:=\{p \in \mathbb {P}: \exists y \in p: y \supseteq x\}$
is open dense in
$\mathcal {D}_x:=\{p \in \mathbb {P}: \exists y \in p: y \supseteq x\}$
is open dense in
![]() $\mathbb {P}$
, by adding
$\mathbb {P}$
, by adding
![]() $\bigcup p \cup x$
to the p in question. Thus,
$\bigcup p \cup x$
to the p in question. Thus,
![]() $\mathbb {Q}^{*}$
is indeed cofinal in
$\mathbb {Q}^{*}$
is indeed cofinal in
![]() $[\mu ]^{{<}\beta }$
. Well-foundedness of
$[\mu ]^{{<}\beta }$
. Well-foundedness of
![]() $\mathbb {Q}^{*}$
follows from H being directed. By the same reason, we have that for every
$\mathbb {Q}^{*}$
follows from H being directed. By the same reason, we have that for every
![]() $x \in \mathbb {Q}^{*}: \{y \in \mathbb {Q}^{*}: y \subseteq x\} \subseteq p$
, where
$x \in \mathbb {Q}^{*}: \{y \in \mathbb {Q}^{*}: y \subseteq x\} \subseteq p$
, where
![]() $p \in H$
is any condition containing x. Thus
$p \in H$
is any condition containing x. Thus
![]() $|\{y \in \mathbb {Q}^{*}: y \subseteq x\}| < \beta $
.
$|\{y \in \mathbb {Q}^{*}: y \subseteq x\}| < \beta $
.
It remains to show (iii) and (iv). In order to verify
![]() $\mathfrak {b}(\mathbb {Q}^{*})=\beta $
and
$\mathfrak {b}(\mathbb {Q}^{*})=\beta $
and
![]() $\mathfrak {d}(\mathbb {Q}^{*})=\mu $
, it suffices, by Fact 5, to verify
$\mathfrak {d}(\mathbb {Q}^{*})=\mu $
, it suffices, by Fact 5, to verify
![]() $\mathfrak {b}(([\mu ]^{<\beta }, \subseteq ))= \beta $
and
$\mathfrak {b}(([\mu ]^{<\beta }, \subseteq ))= \beta $
and
![]() $\mathfrak {d}(([\mu ]^{<\beta }, \subseteq ))=\mu $
in
$\mathfrak {d}(([\mu ]^{<\beta }, \subseteq ))=\mu $
in
![]() $\mathbf {V}[H]$
. To check the first statement, note that by regularity of
$\mathbf {V}[H]$
. To check the first statement, note that by regularity of
![]() $\beta $
, every
$\beta $
, every
![]() $B \subseteq [\mu ]^{<\beta }$
of cardinality
$B \subseteq [\mu ]^{<\beta }$
of cardinality
![]() ${<}\beta $
is bounded. On the other hand, for any
${<}\beta $
is bounded. On the other hand, for any
![]() $X \in [\mu ]^{\beta }$
, the set
$X \in [\mu ]^{\beta }$
, the set
![]() $\{\{\eta \}: \eta \in X\}$
is unbounded, which yields
$\{\{\eta \}: \eta \in X\}$
is unbounded, which yields
![]() $\mathfrak {b}(([\mu ]^{<\beta }, \subseteq ))= \beta $
.
$\mathfrak {b}(([\mu ]^{<\beta }, \subseteq ))= \beta $
.
Similarly, any
![]() $D \subseteq [\mu ]^{<\beta }$
of cardinality
$D \subseteq [\mu ]^{<\beta }$
of cardinality
![]() ${<}\mu $
cannot be dominating, since
${<}\mu $
cannot be dominating, since
![]() $\bigcup D \neq \mu $
. This gives us
$\bigcup D \neq \mu $
. This gives us
![]() $\mathfrak {d}([\mu ]^{<\beta })\geq \mu $
. The reverse inequality holds because
$\mathfrak {d}([\mu ]^{<\beta })\geq \mu $
. The reverse inequality holds because
![]() $|[\mu ]^{<\beta }|=\mu $
, which follows by the assumption
$|[\mu ]^{<\beta }|=\mu $
, which follows by the assumption
![]() $\text {cf}(\mu )\geq \beta $
and by the
$\text {cf}(\mu )\geq \beta $
and by the
![]() $\mathsf {GCH}$
in
$\mathsf {GCH}$
in
![]() $\mathbf {V}$
. Since
$\mathbf {V}$
. Since
![]() $\mathbb {Q}^{*}$
is itself cofinal, this also yields
$\mathbb {Q}^{*}$
is itself cofinal, this also yields
![]() $|\mathbb {Q}^{*}|=\mu $
.
$|\mathbb {Q}^{*}|=\mu $
.
We now fix some
![]() $\mathbb {P}$
-generic H and designate
$\mathbb {P}$
-generic H and designate
![]() $\mathbf {W}:=\mathbf {V}[H]$
as the new ground model. Note that since
$\mathbf {W}:=\mathbf {V}[H]$
as the new ground model. Note that since
![]() $\mathbb {P}$
is
$\mathbb {P}$
is
![]() $\beta $
-closed, the
$\beta $
-closed, the
![]() $\mathsf {GCH}$
still holds at all cardinals below
$\mathsf {GCH}$
still holds at all cardinals below
![]() $\beta $
and
$\beta $
and
![]() $\rho ^{\kappa }=\rho $
for all
$\rho ^{\kappa }=\rho $
for all
![]() $\rho $
with
$\rho $
with
![]() $\text {cf}(\rho )>\kappa $
.
$\text {cf}(\rho )>\kappa $
.
Definition 13 (see [Reference Cummings and Shelah3, Theorem 1])
Let
![]() $\mathbb {Q}$
be any well-founded partially ordered set. Extend
$\mathbb {Q}$
be any well-founded partially ordered set. Extend
![]() $\mathbb {Q}$
to
$\mathbb {Q}$
to
![]() $\mathbb {Q}\cup \{\text {top}\}$
, where
$\mathbb {Q}\cup \{\text {top}\}$
, where
![]() $\forall a \in \mathbb {Q}:\text {top}> a$
. Denote by
$\forall a \in \mathbb {Q}:\text {top}> a$
. Denote by
![]() $\mathbb {Q}_a$
the partial order
$\mathbb {Q}_a$
the partial order
![]() $\mathbb {Q}_{a}:=\{b \in \mathbb {Q}: b < a\}$
, so that
$\mathbb {Q}_{a}:=\{b \in \mathbb {Q}: b < a\}$
, so that
![]() $\mathbb {Q}=\mathbb {Q}_{\text {top}}$
. By induction, we define for each
$\mathbb {Q}=\mathbb {Q}_{\text {top}}$
. By induction, we define for each
![]() $a \in \mathbb {Q} \cup \{\text {top}\}$
the forcing notion
$a \in \mathbb {Q} \cup \{\text {top}\}$
the forcing notion
![]() $\mathbb {D}(\mathbb {Q}_a)$
. Assume
$\mathbb {D}(\mathbb {Q}_a)$
. Assume
![]() $\mathbb {D}(\mathbb {Q}_b)$
is already defined for all
$\mathbb {D}(\mathbb {Q}_b)$
is already defined for all
![]() $b < a$
. We let p be a
$b < a$
. We let p be a
![]() $\mathbb {D}(\mathbb {Q}_a)$
-condition iff:
$\mathbb {D}(\mathbb {Q}_a)$
-condition iff:
-
(i) p is a function with
 $\text {dom}(p)\in [\mathbb {Q}_{a}]^{{<}\kappa }$
.
$\text {dom}(p)\in [\mathbb {Q}_{a}]^{{<}\kappa }$
. -
(ii) For each
 $b \in \text {dom}(p): p(b)=\langle s,\dot {f}\rangle $
, where
$b \in \text {dom}(p): p(b)=\langle s,\dot {f}\rangle $
, where
 $s\in {^{{<}\kappa }}\kappa $
and
$s\in {^{{<}\kappa }}\kappa $
and
 $\dot {f}$
is a nice
$\dot {f}$
is a nice
 $\mathbb {D}(\mathbb {Q}_b)$
-name for an element of
$\mathbb {D}(\mathbb {Q}_b)$
-name for an element of
 $\kappa ^\kappa $
. That is,
$\kappa ^\kappa $
. That is,
 $\dot f$
is of the form
$\dot f$
is of the form
 ${\dot f=\bigcup _{\langle \alpha _1, \alpha _2\rangle \in \kappa \times \kappa }\{\text {op}(\check {\alpha }_1, \check {\alpha }_2)\} \times A_{\langle \alpha _1, \alpha _2 \rangle }}$
, where
${\dot f=\bigcup _{\langle \alpha _1, \alpha _2\rangle \in \kappa \times \kappa }\{\text {op}(\check {\alpha }_1, \check {\alpha }_2)\} \times A_{\langle \alpha _1, \alpha _2 \rangle }}$
, where
 $A_{\langle \alpha _1, \alpha _2 \rangle }$
is an antichain in
$A_{\langle \alpha _1, \alpha _2 \rangle }$
is an antichain in
 $\mathbb {D}(\mathbb {Q}_b)$
and
$\mathbb {D}(\mathbb {Q}_b)$
and
 $\Vdash _{\mathbb {D}(\mathbb {Q}_b)} \dot f \in {\check {\kappa }^\kappa }$
.
$\Vdash _{\mathbb {D}(\mathbb {Q}_b)} \dot f \in {\check {\kappa }^\kappa }$
.
Let
![]() $q \leq p$
iff
$q \leq p$
iff
-
(a)
 $\text {dom}(p) \subseteq \text {dom}(q)$
,
$\text {dom}(p) \subseteq \text {dom}(q)$
, -
(b) For all
 $b \in \text {dom}(p)$
, if
$b \in \text {dom}(p)$
, if
 $p(b)=\langle s, \dot {f}\rangle $
and
$p(b)=\langle s, \dot {f}\rangle $
and
 $q(b)=\langle t, \dot {g}\rangle $
, then
$q(b)=\langle t, \dot {g}\rangle $
, then
 $s\subseteq t$
and
$s\subseteq t$
and  $$\begin{align*}q|_{\mathbb{Q}_b}\Vdash_{\mathbb{D}(\mathbb{Q}_b)} \begin{cases} \forall \eta \in \kappa: \dot{f}(\eta) \leq \dot{g}(\eta) \;\;\text{and}\\ \forall \eta \in \text{dom}(t)\setminus \text{dom}(s): t(\eta)> \dot{f}(\eta). \end{cases} \end{align*}$$
$$\begin{align*}q|_{\mathbb{Q}_b}\Vdash_{\mathbb{D}(\mathbb{Q}_b)} \begin{cases} \forall \eta \in \kappa: \dot{f}(\eta) \leq \dot{g}(\eta) \;\;\text{and}\\ \forall \eta \in \text{dom}(t)\setminus \text{dom}(s): t(\eta)> \dot{f}(\eta). \end{cases} \end{align*}$$
Finally,
![]() $\mathbb {D}(\mathbb {Q})=\mathbb {D}(\mathbb {Q}_{\text {top}})$
.
$\mathbb {D}(\mathbb {Q})=\mathbb {D}(\mathbb {Q}_{\text {top}})$
.
Lemma 7. Let
![]() $\mathbb {Q}$
be any well-founded partial order. Then the following holds.
$\mathbb {Q}$
be any well-founded partial order. Then the following holds.
-
(i)
 $\mathbb {D}(\mathbb {Q})$
is
$\mathbb {D}(\mathbb {Q})$
is
 $\kappa $
-closed.
$\kappa $
-closed. -
(ii)
 $\mathbb {D}(\mathbb {Q})$
satisfies the
$\mathbb {D}(\mathbb {Q})$
satisfies the
 $\kappa ^{+}$
-c.c.
$\kappa ^{+}$
-c.c. -
(iii) Let
 $\mathbb {A}\subseteq \mathbb {Q}$
be downward-closed, i.e., for all
$\mathbb {A}\subseteq \mathbb {Q}$
be downward-closed, i.e., for all
 $p \in \mathbb {A}$
and
$p \in \mathbb {A}$
and
 $q \in \mathbb {Q} : q \leq _{\mathbb {Q}}p \implies q \in \mathbb {A}$
. Then
$q \in \mathbb {Q} : q \leq _{\mathbb {Q}}p \implies q \in \mathbb {A}$
. Then
 $\mathbb {D}(\mathbb {A})$
is a complete suborder of
$\mathbb {D}(\mathbb {A})$
is a complete suborder of
 $\mathbb {D}(\mathbb {Q})$
.
$\mathbb {D}(\mathbb {Q})$
. -
(iv) Assume
 $|\mathbb {Q}|^{\kappa } = |\mathbb {Q}| $
. There are at most
$|\mathbb {Q}|^{\kappa } = |\mathbb {Q}| $
. There are at most
 $|\mathbb {Q}|$
many nice
$|\mathbb {Q}|$
many nice
 $\mathbb {D}(\mathbb {Q})$
-names for subsets of
$\mathbb {D}(\mathbb {Q})$
-names for subsets of
 $\kappa $
.
$\kappa $
.
Proof. Parts (i) and (ii) are proved in [Reference Cummings and Shelah3, Claims 1 and 2]. Part (iii) is straightfoward to check. For part (iv), let
![]() $|\mathbb {Q}|= \rho $
with
$|\mathbb {Q}|= \rho $
with
![]() $\rho ^\kappa =\rho $
and let
$\rho ^\kappa =\rho $
and let
![]() $a \in \mathbb {Q}\cup \{\text {top}\}$
. Assume by induction that for all
$a \in \mathbb {Q}\cup \{\text {top}\}$
. Assume by induction that for all
![]() $b < a$
there are at most
$b < a$
there are at most
![]() $\rho $
many nice
$\rho $
many nice
![]() $\mathbb {D}(\mathbb {Q}_b)$
-names for subsets of
$\mathbb {D}(\mathbb {Q}_b)$
-names for subsets of
![]() $\kappa $
. In particular, there are at most
$\kappa $
. In particular, there are at most
![]() $\rho $
many nice
$\rho $
many nice
![]() $\mathbb {D}(\mathbb {Q}_b)$
-names for elements of
$\mathbb {D}(\mathbb {Q}_b)$
-names for elements of
![]() $\kappa ^\kappa $
. Since
$\kappa ^\kappa $
. Since
![]() $\mathbb {D}(\mathbb {Q}_a)$
satisfies the
$\mathbb {D}(\mathbb {Q}_a)$
satisfies the
![]() $\kappa ^{+}$
-c.c., the number of nice
$\kappa ^{+}$
-c.c., the number of nice
![]() $\mathbb {D}(\mathbb {Q}_a)$
-names for subsets of
$\mathbb {D}(\mathbb {Q}_a)$
-names for subsets of
![]() $\kappa $
is bounded by
$\kappa $
is bounded by
![]() $|\mathbb {D}(\mathbb {Q}_a)|^{\kappa }$
. Note that
$|\mathbb {D}(\mathbb {Q}_a)|^{\kappa }$
. Note that
![]() $|\mathbb {D}(\mathbb {Q}_a)| \leq |\mathbb {Q}_a|^{{<}\kappa } \cdot \kappa ^{<\kappa } \cdot \rho ^{{<}\kappa }$
by the induction hypothesis. This is at most
$|\mathbb {D}(\mathbb {Q}_a)| \leq |\mathbb {Q}_a|^{{<}\kappa } \cdot \kappa ^{<\kappa } \cdot \rho ^{{<}\kappa }$
by the induction hypothesis. This is at most
![]() $\rho $
, because
$\rho $
, because
![]() $\mathbb {Q}_a\subseteq \mathbb {Q}$
and
$\mathbb {Q}_a\subseteq \mathbb {Q}$
and
![]() $\rho ^{{<}\kappa }=\rho $
, which finally yields that there are at most
$\rho ^{{<}\kappa }=\rho $
, which finally yields that there are at most
![]() $\rho ^\kappa =\rho $
nice
$\rho ^\kappa =\rho $
nice
![]() $\mathbb {D}(\mathbb {Q}_a)$
-names for subsets of
$\mathbb {D}(\mathbb {Q}_a)$
-names for subsets of
![]() $\kappa $
.
$\kappa $
.
Lemma 8. [Reference Cummings and Shelah3, Theorem 1]
Let
![]() $\mathbb {Q}$
be any well-founded partial order with
$\mathbb {Q}$
be any well-founded partial order with
![]() $\mathfrak {b}(\mathbb {Q})\geq \kappa ^{+}$
. In any
$\mathfrak {b}(\mathbb {Q})\geq \kappa ^{+}$
. In any
![]() $\mathbb {D}(\mathbb {Q})$
-generic extension,
$\mathbb {D}(\mathbb {Q})$
-generic extension,
![]() $\mathbb {Q}$
can be cofinally embedded into
$\mathbb {Q}$
can be cofinally embedded into
![]() $(\kappa ^\kappa , \leq ^{*})$
.
$(\kappa ^\kappa , \leq ^{*})$
.
Corollary 4. Let G be
![]() $\mathbb {D}(\mathbb {Q}^{*})$
-generic over
$\mathbb {D}(\mathbb {Q}^{*})$
-generic over
![]() $\mathbf {W}$
, where
$\mathbf {W}$
, where
![]() $\mathbb {Q}^{*}$
is from Lemma 6. Then,
$\mathbb {Q}^{*}$
is from Lemma 6. Then,
Proof. We have
![]() $|\mathbb {Q}^{*}|=\mu $
by Lemma 6 (iv), which implies by Lemma 7 (iv) that there are at most
$|\mathbb {Q}^{*}|=\mu $
by Lemma 6 (iv), which implies by Lemma 7 (iv) that there are at most
![]() $\mu $
many nice
$\mu $
many nice
![]() $\mathbb {D}(\mathbb {Q}^{*})$
-names for subsets of
$\mathbb {D}(\mathbb {Q}^{*})$
-names for subsets of
![]() $\kappa $
. Thus,
$\kappa $
. Thus,
![]() $\mathbf {W}[G]\models 2^\kappa \leq \mu $
. In order to verify the remaining claims, it suffices by the above Lemma 8 and by Fact 5 to check that
$\mathbf {W}[G]\models 2^\kappa \leq \mu $
. In order to verify the remaining claims, it suffices by the above Lemma 8 and by Fact 5 to check that
![]() $\mathfrak {b}(\mathbb {Q}^{*})=\beta $
and
$\mathfrak {b}(\mathbb {Q}^{*})=\beta $
and
![]() $\mathfrak {d}(\mathbb {Q}^{*})=\mu $
still holds in
$\mathfrak {d}(\mathbb {Q}^{*})=\mu $
still holds in
![]() $\mathbf {W}[G]$
. However, this very easily follows from
$\mathbf {W}[G]$
. However, this very easily follows from
![]() $\mathbb {D}(\mathbb {Q}^{*})$
satisfying the
$\mathbb {D}(\mathbb {Q}^{*})$
satisfying the
![]() $\kappa ^{+}$
-c.c.
$\kappa ^{+}$
-c.c.
Proposition 2. Let G be
![]() $\mathbb {D}(\mathbb {Q}^{*})$
-generic over
$\mathbb {D}(\mathbb {Q}^{*})$
-generic over
![]() $\mathbf {W}$
. Then
$\mathbf {W}$
. Then
![]() $\mathbf {W}[G]\models \mathfrak {sp}(\mathfrak {t}(\kappa )) \subseteq [\kappa ^{+}, \beta ]$
.
$\mathbf {W}[G]\models \mathfrak {sp}(\mathfrak {t}(\kappa )) \subseteq [\kappa ^{+}, \beta ]$
.
Proof. Assume towards a contradiction that
![]() $\langle a_\xi : \xi \in \beta ^{+}\rangle $
is a strictly
$\langle a_\xi : \xi \in \beta ^{+}\rangle $
is a strictly
![]() $\supseteq ^{*}$
-descending sequence in
$\supseteq ^{*}$
-descending sequence in
![]() $\mathbf {W}[G]$
. For each
$\mathbf {W}[G]$
. For each
![]() $\xi \in \beta ^{+}$
, let
$\xi \in \beta ^{+}$
, let
![]() $\dot {a}_\xi =\bigcup _{\alpha \in \kappa }\{\check {\alpha }\}\times A_\alpha ^\xi $
be a nice
$\dot {a}_\xi =\bigcup _{\alpha \in \kappa }\{\check {\alpha }\}\times A_\alpha ^\xi $
be a nice
![]() $\mathbb {D}(\mathbb {Q}^{*})$
-name for
$\mathbb {D}(\mathbb {Q}^{*})$
-name for
![]() $a_\xi $
. Assume
$a_\xi $
. Assume
![]() $p_0\in \mathbb {D}(\mathbb {Q}^{*})$
is such that for all
$p_0\in \mathbb {D}(\mathbb {Q}^{*})$
is such that for all
![]() $\xi < \xi ' < \beta ^{+}: p_0 \Vdash _{\mathbb {D}(\mathbb {Q}^{*})} \dot {a}_\xi \supsetneq ^{*} \dot {a}_{\xi '}$
.
$\xi < \xi ' < \beta ^{+}: p_0 \Vdash _{\mathbb {D}(\mathbb {Q}^{*})} \dot {a}_\xi \supsetneq ^{*} \dot {a}_{\xi '}$
.
Define for every
![]() $\xi \in \beta ^{+}$
the set
$\xi \in \beta ^{+}$
the set
which is a subset of
![]() $\mu $
of size
$\mu $
of size
![]() ${<}\beta $
. Since
${<}\beta $
. Since
![]() $\mathbb {Q}^{*}$
is cofinal in
$\mathbb {Q}^{*}$
is cofinal in
![]() $[\mu ]^{<\beta }$
, we find for each
$[\mu ]^{<\beta }$
, we find for each
![]() $\xi \in \beta ^{+}$
some
$\xi \in \beta ^{+}$
some
![]() $D_\xi \supseteq d_\xi $
in
$D_\xi \supseteq d_\xi $
in
![]() $\mathbb {Q}^{*}$
. As noted before, the
$\mathbb {Q}^{*}$
. As noted before, the
![]() $\mathsf {GCH}$
holds in
$\mathsf {GCH}$
holds in
![]() $\mathbf {W}$
below
$\mathbf {W}$
below
![]() $\beta $
and we may therefore apply the
$\beta $
and we may therefore apply the
![]() $\Delta $
-system Lemma to the family
$\Delta $
-system Lemma to the family
![]() $\{D_\xi : \xi \in \beta ^{+}\}$
to obtain some
$\{D_\xi : \xi \in \beta ^{+}\}$
to obtain some
![]() $X \subseteq \beta ^{+}$
of cardinality
$X \subseteq \beta ^{+}$
of cardinality
![]() $\beta ^{+}$
and a root R. Set
$\beta ^{+}$
and a root R. Set
![]() $\mathbb {Q}^{*}_\xi :=\{y \in \mathbb {Q}^{*}: y \subseteq D_\xi \}$
and
$\mathbb {Q}^{*}_\xi :=\{y \in \mathbb {Q}^{*}: y \subseteq D_\xi \}$
and
![]() $\mathbb {R}:=\{y \in \mathbb {Q}^{*}: y \subseteq R\}$
. Note that
$\mathbb {R}:=\{y \in \mathbb {Q}^{*}: y \subseteq R\}$
. Note that
![]() $\mathbb {R}$
is the root of the
$\mathbb {R}$
is the root of the
![]() $\mathbb {Q}^{*}_\xi $
. By Lemma 6 (ii), we have
$\mathbb {Q}^{*}_\xi $
. By Lemma 6 (ii), we have
![]() $| \mathbb {Q}^{*}_\xi |<\beta $
, and we may therefore assume by the pigeonhole principle that
$| \mathbb {Q}^{*}_\xi |<\beta $
, and we may therefore assume by the pigeonhole principle that
![]() $\forall \xi \in X: |\mathbb {Q}^{*}_\xi |=\theta < \beta $
.
$\forall \xi \in X: |\mathbb {Q}^{*}_\xi |=\theta < \beta $
.
Claim 5. There exists
![]() $X'\subseteq X$
of cardinality
$X'\subseteq X$
of cardinality
![]() $\beta ^{+}$
such that for all
$\beta ^{+}$
such that for all
![]() $\xi , \xi '\in X'$
, there is an order-preserving isomorphism
$\xi , \xi '\in X'$
, there is an order-preserving isomorphism
![]() $\psi _{\xi , \xi '}: \mathbb {Q}^{*}_\xi \to \mathbb {Q}^{*}_{\xi '}$
with
$\psi _{\xi , \xi '}: \mathbb {Q}^{*}_\xi \to \mathbb {Q}^{*}_{\xi '}$
with
![]() $\psi _{\xi , \xi '}|_{\mathbb {R}}=\text {id}$
.
$\psi _{\xi , \xi '}|_{\mathbb {R}}=\text {id}$
.
Proof. To see this, let L be some set of cardinality
![]() $|\mathbb {Q}^{*}_\xi \setminus \mathbb {R}|$
disjoint from
$|\mathbb {Q}^{*}_\xi \setminus \mathbb {R}|$
disjoint from
![]() $\mathbb {R}$
. For each
$\mathbb {R}$
. For each
![]() $\xi \in X$
, we can map
$\xi \in X$
, we can map
![]() $\mathbb {Q}^{*}_\xi $
bijectively to
$\mathbb {Q}^{*}_\xi $
bijectively to
![]() $L \cup \mathbb {R}$
, such that this bijection restricted to
$L \cup \mathbb {R}$
, such that this bijection restricted to
![]() $\mathbb {R}$
is the identity. This bijection induces a partial order on
$\mathbb {R}$
is the identity. This bijection induces a partial order on
![]() $L \cup \mathbb {R}$
. Since there are at most
$L \cup \mathbb {R}$
. Since there are at most
![]() $2^\theta \leq \beta $
many partial orders on
$2^\theta \leq \beta $
many partial orders on
![]() $L \cup \mathbb {R}$
, we find the desired
$L \cup \mathbb {R}$
, we find the desired
![]() $X'$
as well as the isomorphisms
$X'$
as well as the isomorphisms
![]() $\psi _{\xi , \xi '}$
by the pigeonhole principle.
$\psi _{\xi , \xi '}$
by the pigeonhole principle.
Define the downward-closed partially ordered set
![]() $\mathbb {A}:=\bigcup _{\xi \in X'}\mathbb {Q}^{*}_{\xi }$
. Note that by definition of
$\mathbb {A}:=\bigcup _{\xi \in X'}\mathbb {Q}^{*}_{\xi }$
. Note that by definition of
![]() $D_\xi $
,
$D_\xi $
,
![]() $\dot a_\xi $
is a nice
$\dot a_\xi $
is a nice
![]() $\mathbb {D}(\mathbb {Q}^{*}_\xi )$
-name and thus a nice
$\mathbb {D}(\mathbb {Q}^{*}_\xi )$
-name and thus a nice
![]() $\mathbb {D}(\mathbb {A})$
-name. Furthermore,
$\mathbb {D}(\mathbb {A})$
-name. Furthermore,
![]() $p_0$
is a
$p_0$
is a
![]() $\mathbb {D}(\mathbb {R})$
-condition. For a fixed
$\mathbb {D}(\mathbb {R})$
-condition. For a fixed
![]() $\xi _0 \in X'$
, the isomorphism
$\xi _0 \in X'$
, the isomorphism
![]() $\psi _{\xi , \xi _0}$
extends to an automorphism of order 2 of
$\psi _{\xi , \xi _0}$
extends to an automorphism of order 2 of
![]() $\mathbb {A}$
, which we denote by
$\mathbb {A}$
, which we denote by
![]() $\psi _{\xi }$
. This automorphism
$\psi _{\xi }$
. This automorphism
![]() $\psi _{\xi }$
naturally induces an automorphism
$\psi _{\xi }$
naturally induces an automorphism
![]() $\varphi _{\xi }$
of
$\varphi _{\xi }$
of
![]() $\mathbb {D}(\mathbb {A})$
in the obvious way: Let
$\mathbb {D}(\mathbb {A})$
in the obvious way: Let
![]() ${a \in \mathbb {A}\cup \{\text {top}\}}$
and assume by induction that for every
${a \in \mathbb {A}\cup \{\text {top}\}}$
and assume by induction that for every
![]() $b< a$
, the isomorphism
$b< a$
, the isomorphism
has been defined (note the abuse of notation). In particular, this isomorphism extends to
![]() $\mathbb {D}(\mathbb {A}_b)$
-names. Now let p be any
$\mathbb {D}(\mathbb {A}_b)$
-names. Now let p be any
![]() $\mathbb {D}(\mathbb {A}_a)$
-condition. We write for every
$\mathbb {D}(\mathbb {A}_a)$
-condition. We write for every
![]() $b \in \text {dom}(p): p(b)=\langle s(b), \dot f(b)\rangle $
, and define
$b \in \text {dom}(p): p(b)=\langle s(b), \dot f(b)\rangle $
, and define
 $$\begin{align*}\varphi_{\xi}|_{\mathbb{D}(\mathbb{A}_a)}(p):=q, \;\text{where}\; \begin{cases} \text{dom}(q):=\psi_{\xi}[\text{dom}(p)] \;\;\text{and}\\ \forall \psi_{\xi}(b) \in \text{dom}(q): q(\psi_{\xi}(b)):= \langle s(b), \varphi_{\xi}|_{\mathbb{D}(\mathbb{A}_b)}(\dot f)\rangle \end{cases} \end{align*}$$
$$\begin{align*}\varphi_{\xi}|_{\mathbb{D}(\mathbb{A}_a)}(p):=q, \;\text{where}\; \begin{cases} \text{dom}(q):=\psi_{\xi}[\text{dom}(p)] \;\;\text{and}\\ \forall \psi_{\xi}(b) \in \text{dom}(q): q(\psi_{\xi}(b)):= \langle s(b), \varphi_{\xi}|_{\mathbb{D}(\mathbb{A}_b)}(\dot f)\rangle \end{cases} \end{align*}$$
It follows by induction that
![]() $\varphi _{\xi }$
is an automorphism and that
$\varphi _{\xi }$
is an automorphism and that
![]() $\varphi _{\xi }|_{\mathbb {D}(\mathbb {R})}=\text {id}$
.
$\varphi _{\xi }|_{\mathbb {D}(\mathbb {R})}=\text {id}$
.
Note that
![]() $\varphi _{\xi }(\dot a_\xi )$
is a nice
$\varphi _{\xi }(\dot a_\xi )$
is a nice
![]() $\mathbb {D}(\mathbb {Q}^{*}_{\xi _0})$
-name and that by Lemma 7 (iv), there are at most
$\mathbb {D}(\mathbb {Q}^{*}_{\xi _0})$
-name and that by Lemma 7 (iv), there are at most
![]() $|\mathbb {Q}^{*}_{\xi _0}|<\beta $
many nice
$|\mathbb {Q}^{*}_{\xi _0}|<\beta $
many nice
![]() $\mathbb {D}(\mathbb {Q}^{*}_{\xi _0})$
-names for subsets of
$\mathbb {D}(\mathbb {Q}^{*}_{\xi _0})$
-names for subsets of
![]() $\kappa $
. Thus, we can extract
$\kappa $
. Thus, we can extract
![]() $X" \subseteq X'$
of cardinality
$X" \subseteq X'$
of cardinality
![]() $\beta ^{+}$
such that
$\beta ^{+}$
such that
![]() $\varphi _{\xi }(\dot a_\xi )$
is the same nice
$\varphi _{\xi }(\dot a_\xi )$
is the same nice
![]() $\mathbb {D}(\mathbb {Q}^{*}_{\xi _0})$
-name for all
$\mathbb {D}(\mathbb {Q}^{*}_{\xi _0})$
-name for all
![]() $\xi \in X"$
.
$\xi \in X"$
.
Fix
![]() $\xi < \xi ' \in X"\setminus \{\xi _0\}$
and define the automorphism
$\xi < \xi ' \in X"\setminus \{\xi _0\}$
and define the automorphism
![]() $\chi _{\xi , \xi '}:=\varphi _{\xi '} \circ \varphi _{\xi } \circ \varphi _{\xi '}$
of
$\chi _{\xi , \xi '}:=\varphi _{\xi '} \circ \varphi _{\xi } \circ \varphi _{\xi '}$
of
![]() $\mathbb {A}$
. By construction,
$\mathbb {A}$
. By construction,
![]() $\chi _{\xi , \xi '}(\dot a_\xi )=\dot a_{\xi '}$
,
$\chi _{\xi , \xi '}(\dot a_\xi )=\dot a_{\xi '}$
,
![]() $\chi _{\xi , \xi '}(\dot a_{\xi '})=\dot a_{\xi }$
and
$\chi _{\xi , \xi '}(\dot a_{\xi '})=\dot a_{\xi }$
and
![]() $\chi _{\xi , \xi '}(p_0)=p_0$
. Since
$\chi _{\xi , \xi '}(p_0)=p_0$
. Since
![]() $\mathbb {D}(\mathbb {A})$
is a complete suborder of
$\mathbb {D}(\mathbb {A})$
is a complete suborder of
![]() $\mathbb {D}(\mathbb {Q}^{*})$
by Lemma 7 (iii), we have
$\mathbb {D}(\mathbb {Q}^{*})$
by Lemma 7 (iii), we have
![]() $p_0 \Vdash _{\mathbb {D}(\mathbb {A})} \dot a_\xi \supsetneq ^{*} \dot a_{\xi '} $
, which yields the contradiction
$p_0 \Vdash _{\mathbb {D}(\mathbb {A})} \dot a_\xi \supsetneq ^{*} \dot a_{\xi '} $
, which yields the contradiction
![]() $p_0 \Vdash _{\mathbb {D}(\mathbb {A})} \dot a_{\xi '} \supsetneq ^{*} \dot a_{\xi } \land \dot a_{\xi } \supsetneq ^{*} \dot a_{\xi '}$
, just as in the proof of Theorem 1.
$p_0 \Vdash _{\mathbb {D}(\mathbb {A})} \dot a_{\xi '} \supsetneq ^{*} \dot a_{\xi } \land \dot a_{\xi } \supsetneq ^{*} \dot a_{\xi '}$
, just as in the proof of Theorem 1.
Together with Lemma 1, the above Theorem yields the following corollary.
Corollary 5. Let
![]() $\kappa < \beta $
be regular uncountable and let
$\kappa < \beta $
be regular uncountable and let
![]() $\mu $
be such that
$\mu $
be such that
![]() $\text {cf}(\mu )\geq \beta $
. Then, consistently,
$\text {cf}(\mu )\geq \beta $
. Then, consistently,
As a final remark, note that by Lemma 1 and Lemma 2, the upper bound given by Theorem 4 is tight, in the sense that there always exists a
![]() $\kappa $
-tower of length
$\kappa $
-tower of length
![]() $\mathfrak {b}(\kappa )$
, if
$\mathfrak {b}(\kappa )$
, if
![]() $\kappa $
is uncountable or if
$\kappa $
is uncountable or if
![]() $\mathfrak {b}(\omega )<\mathfrak {d}(\omega )$
. If both
$\mathfrak {b}(\omega )<\mathfrak {d}(\omega )$
. If both
![]() $\kappa =\omega $
and
$\kappa =\omega $
and
![]() $\beta =\mu $
however, a well-founded cofinal subset of the partial order
$\beta =\mu $
however, a well-founded cofinal subset of the partial order
![]() $([\beta ]^{<\beta }, \subseteq )$
as in Lemma 6 is given by the well-ordered set
$([\beta ]^{<\beta }, \subseteq )$
as in Lemma 6 is given by the well-ordered set
![]() $\beta $
, in which case we have a simple finite-support,
$\beta $
, in which case we have a simple finite-support,
![]() $\beta $
-stage linear iteration of Hechler forcing, and thus no
$\beta $
-stage linear iteration of Hechler forcing, and thus no
![]() $\omega $
-tower of length
$\omega $
-tower of length
![]() $\beta =\mathfrak {b}(\omega )$
in the extension, as was shown by Baumgartner and Dordal [Reference Baumgartner and Dordal2, Theorem 4.1]
$\beta =\mathfrak {b}(\omega )$
in the extension, as was shown by Baumgartner and Dordal [Reference Baumgartner and Dordal2, Theorem 4.1]
5. Open problems
Our first question is whether a global version of the result in Section 4 is consistent. More concretely:
Question 1. Let E be an index function attaining values
![]() $E(\kappa )=\langle \beta (\kappa ), \mu (\kappa )\rangle $
, such that
$E(\kappa )=\langle \beta (\kappa ), \mu (\kappa )\rangle $
, such that
![]() $\kappa ^{+} \leq \text {cf}(\beta (\kappa ))=\beta (\kappa ) \leq \text {cf}(\mu (\kappa ))$
for every
$\kappa ^{+} \leq \text {cf}(\beta (\kappa ))=\beta (\kappa ) \leq \text {cf}(\mu (\kappa ))$
for every
![]() $\kappa \in \text {dom}(E)$
and such that
$\kappa \in \text {dom}(E)$
and such that
![]() $\kappa < \kappa ' \implies \mu (\kappa )\leq \mu (\kappa ')$
. Is it consistent that for every
$\kappa < \kappa ' \implies \mu (\kappa )\leq \mu (\kappa ')$
. Is it consistent that for every
![]() $\kappa \in \text {dom}(E): \mathfrak {sp}(\mathfrak {t}(\kappa )) \subseteq [\kappa ^{+}, \mathfrak {b}(\kappa )]$
, where
$\kappa \in \text {dom}(E): \mathfrak {sp}(\mathfrak {t}(\kappa )) \subseteq [\kappa ^{+}, \mathfrak {b}(\kappa )]$
, where
![]() $\mathfrak {b}(\kappa )=\beta (\kappa )$
and
$\mathfrak {b}(\kappa )=\beta (\kappa )$
and
![]() $2^\kappa =\mu (\kappa )$
?
$2^\kappa =\mu (\kappa )$
?
Cummings and Shelah [Reference Cummings and Shelah3, Theorem 4] have shown that the global separation of
![]() $\mathfrak {b}(\kappa )$
and
$\mathfrak {b}(\kappa )$
and
![]() $2^\kappa $
as above is consistent. The issue is whether the bound on the tower spectrum carries over to their construction, which uses an Easton-tail iteration (i.e., a hybrid between Easton-iteration and Easton-product). An analogous question is whether a global non-trivial lower bound on the tower spectrum is consistent, i.e.,
$2^\kappa $
as above is consistent. The issue is whether the bound on the tower spectrum carries over to their construction, which uses an Easton-tail iteration (i.e., a hybrid between Easton-iteration and Easton-product). An analogous question is whether a global non-trivial lower bound on the tower spectrum is consistent, i.e.,
Question 2. To what extent can the characteristic
![]() $\mathfrak {t}(\kappa )$
be controlled globally?
$\mathfrak {t}(\kappa )$
be controlled globally?
Here, the complication lies in the fact that the generalized continuum function and the class function
![]() $\kappa \to \mathfrak {t}(\kappa )$
are strongly correlated: If
$\kappa \to \mathfrak {t}(\kappa )$
are strongly correlated: If
![]() $\kappa \leq \delta < \mathfrak {t}(\kappa )$
, then
$\kappa \leq \delta < \mathfrak {t}(\kappa )$
, then
![]() $2^\delta =2^\kappa $
, as was shown by Shelah and Spasojević [Reference Shelah and Spasojević11, Main Lemma 2.1].
$2^\delta =2^\kappa $
, as was shown by Shelah and Spasojević [Reference Shelah and Spasojević11, Main Lemma 2.1].
Finally, strengthening both of the above questions:
Question 3. Let E be an index function such that
![]() $E(\kappa )$
is a set of regular cardinals for all
$E(\kappa )$
is a set of regular cardinals for all
![]() $\kappa \in \text {dom}(E)$
. Is it consistent that
$\kappa \in \text {dom}(E)$
. Is it consistent that
Acknowledgments
We thank the anonymous referee for their very helpful corrections and suggestions.
Funding
This research was funded in whole or in part by the Austrian Science Fund (FWF) through project START Y1012 [10.55776/Y1012]. The second author would additionally like to thank the Swiss European Mobility Programme (SEMP) for financially supporting his stay at the University of Vienna.