Article contents
Generalizations of the one-dimensional version of the Kruskal-Friedman theorems
Published online by Cambridge University Press: 12 March 2014
Extract
The paper [Schütte + Simpson] deals with the following one-dimensional case of Friedman's extension (see in [Simpson 1]) of Kruskal's theorem ([Kruskal]). Given a natural number n, let Sn+1 be the set of all finite sequences of natural numbers <n + 1. If s1 = (a0,…,ak) ∈Sn+1 and s2 = (b0,…,bm) ∈Sn + 1, then a strictly monotone function f: {0,…, k} → {0,…, m} is called an embedding of s1 into s2 if the following two assertions are satisfied:
1) ai, = bf(i), for all i < k;
2) if f(i) < j < f(i + 1) then bj > bf(i+1), for all i < k, j < m.
Then for every infinite sequence s1, s2,…,sk,… of elements of Sn + 1 there exist indices i < j and an embedding of si into Sj. That is, Sn+1 forms a well-quasi-ordering (wqo) with respect to embeddability. For each n, this statement W(Sn+1) is provable in the standard second order conservative extension of Peano arithmetic. On the other hand, the proof-theoretic strength of the statements W(Sn+1) grows so fast that this formal theory cannot prove the limit statement ∀nW(Sn+1). The appropriate first order 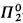 -versions of these combinatory statements preserve their proof-theoretic strength, so that actually one can speak in terms of provability in Peano arithmetic. These are the main conclusions from [Schütte + Simpson].
-versions of these combinatory statements preserve their proof-theoretic strength, so that actually one can speak in terms of provability in Peano arithmetic. These are the main conclusions from [Schütte + Simpson].
We wish to extend this into the transfinite. That is, we take an arbitrary countable ordinal τ > 0 instead of n + 1 and try to obtain an analogous “strong” combinatory statement about finite sequences of ordinals < τ.
Information
- Type
- Research Article
- Information
- Copyright
- Copyright © Association for Symbolic Logic 1989
References
REFERENCES
- 6
- Cited by

