No CrossRef data available.
Article contents
A generalization of forking
Published online by Cambridge University Press: 12 March 2014
Extract
Given a subset A of a fixed saturated model 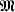 , we let
, we let 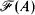 denote the algebra of definable subsets of the domain of M of
denote the algebra of definable subsets of the domain of M of 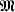 with parameters from A. Then a complete type p over A can be regarded as a measure on
with parameters from A. Then a complete type p over A can be regarded as a measure on 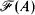 , assigning the value 1 to members of p and 0 to nonmembers. In [5] and [6], Keisler developed a theory of forking concerning probability measures. Therefore it generalizes the ordinary theory. On a different track, we can view the complement of the type p, or the collection of null sets of any measure on
, assigning the value 1 to members of p and 0 to nonmembers. In [5] and [6], Keisler developed a theory of forking concerning probability measures. Therefore it generalizes the ordinary theory. On a different track, we can view the complement of the type p, or the collection of null sets of any measure on 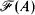 , as ideals on
, as ideals on 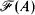 . Moreover, ideals and the pseudometric of a measure form examples of the so-called FN topology. Roughly speaking, an FN topology is one that topologizes the ring structure of a Boolean algebra. Associated with this topology is a special basis, called an FN basis. For
. Moreover, ideals and the pseudometric of a measure form examples of the so-called FN topology. Roughly speaking, an FN topology is one that topologizes the ring structure of a Boolean algebra. Associated with this topology is a special basis, called an FN basis. For 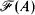 , it is natural to identify such a basis with a collection of partial types approximating a certain type.
, it is natural to identify such a basis with a collection of partial types approximating a certain type.
In this paper, we extend the theory of forking and deal with FN bases (hence ideals in particular). By proving a few results here, we hope to indicate that this extension could become as fruitful as Keisler's theory and hence provide an alternative. Our approach here is more algebraic and less analytic. Unlike [5], methods from nonstandard analysis are not used.
There are two fundamental reasons why the classical theory should be generalized. One is to extend our investigation to unstable theories. (There are no stability assumptions on the theory in the present work.) The other is to study different and more flexible ways of collecting formulas, such as FN basis.
After fixing our notation in §1, we first deal with ideals in §2. We study certain nice extensions. Specifically, we prove the existence of flat nonforking ideals. We then provide a normalization theorem for ideals.
Information
- Type
- Research Article
- Information
- Copyright
- Copyright © Association for Symbolic Logic 1991

