Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by
Crossref.
Rayo, A.
2004.
Frege's correlation.
Analysis,
Vol. 64,
Issue. 2,
p.
119.
Antonelli, Aldo
and
May, Robert
2005.
Frege's Other Program.
Notre Dame Journal of Formal Logic,
Vol. 46,
Issue. 1,
Slater, B. H.
2006.
Grammar and sets.
Australasian Journal of Philosophy,
Vol. 84,
Issue. 1,
p.
59.
Rayo, Agustín
2007.
Plurals.
Philosophy Compass,
Vol. 2,
Issue. 3,
p.
411.
Rayo, Agustín
2008.
On Specifying Truth-Conditions.
The Philosophical Review,
Vol. 117,
Issue. 3,
p.
385.
Rayo, Agustín
2009.
New Waves in Philosophy of Mathematics.
p.
239.
Rayo, Agustín
2009.
The Oxford Handbook of Philosophy of Mathematics and Logic.
p.
203.
Landini, G.
2011.
Logicism and the Problem of Infinity: The Number of Numbers.
Philosophia Mathematica,
Vol. 19,
Issue. 2,
p.
167.
Landini, G.
2011.
Logicism and the Problem of Infinity: The Number of Numbers.
Philosophia Mathematica,
Vol. 19,
Issue. 2,
p.
167.
Yablo, S.
2012.
Explanation, Extrapolation, and Existence.
Mind,
Vol. 121,
Issue. 484,
p.
1007.
Kim, Joongol
2013.
What are numbers?.
Synthese,
Vol. 190,
Issue. 6,
p.
1099.
Rayo, A.
2014.
Nominalism, Trivialism, Logicism.
Philosophia Mathematica,
Kim, Joongol
2015.
A Logical Foundation of Arithmetic.
Studia Logica,
Vol. 103,
Issue. 1,
p.
113.
Soames, Scott
2015.
Reply to critics of the analytic tradition in philosophy vol. 1 the founding giants.
Philosophical Studies,
Vol. 172,
Issue. 6,
p.
1681.
Rayo, A.
2015.
Nominalism, Trivialism, Logicism.
Philosophia Mathematica,
Vol. 23,
Issue. 1,
p.
65.
Beaney, Michael
2015.
Soames on Frege: provoking thoughts.
Philosophical Studies,
Vol. 172,
Issue. 6,
p.
1651.
KLEV, ANSTEN
2018.
THE CONCEPTHORSEIS A CONCEPT.
The Review of Symbolic Logic,
Vol. 11,
Issue. 3,
p.
547.
Vivanco, Melisa
2023.
Numbers as properties.
Synthese,
Vol. 202,
Issue. 4,
Zanetti, Luca
and
Boccuni, Francesca
2025.
Abstractionism.
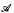 of L (which is true on the intended interpretation of L), and a compositionally recursive transformation Tr defined on formulas of L, and show that they have the following two properties: (a) in a universe with at least ℶn−2 objects, any formula of nth-order (pure or applied) arithmetic can be expressed as a formula of L, and (b) for any sentence
of L (which is true on the intended interpretation of L), and a compositionally recursive transformation Tr defined on formulas of L, and show that they have the following two properties: (a) in a universe with at least ℶn−2 objects, any formula of nth-order (pure or applied) arithmetic can be expressed as a formula of L, and (b) for any sentence 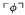 of
of 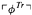 is a second-order sentence containing no arithmetical vocabulary, and
is a second-order sentence containing no arithmetical vocabulary, and