Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by
Crossref.
Visser, Albert
2002.
Substitutions of Σ10-sentences: explorations between intuitionistic propositional logic and intuitionistic arithmetic.
Annals of Pure and Applied Logic,
Vol. 114,
Issue. 1-3,
p.
227.
Ostrin, G. E.
and
Wainer, S. S.
2002.
Proof and System-Reliability.
p.
369.
Moniri, Morteza
2002.
Weak Arithmetics and Kripke Models.
MLQ,
Vol. 48,
Issue. 1,
p.
157.
Moniri, Morteza
2003.
Independence results for weak systems of intuitionistic arithmetic.
Mathematical Logic Quarterly,
Vol. 49,
Issue. 3,
p.
250.
Ostrin, G.E.
and
Wainer, S.S.
2005.
Elementary arithmetic.
Annals of Pure and Applied Logic,
Vol. 133,
Issue. 1-3,
p.
275.
Artemov, Sergei N.
and
Beklemishev, Lev D.
2005.
Handbook of Philosophical Logic, 2nd Edition.
Vol. 13,
Issue. ,
p.
189.
Beklemishev, Lev
and
Visser, Albert
2006.
Mathematical Problems from Applied Logic I.
Vol. 4,
Issue. ,
p.
77.
Fleischmann, Jonathan
2010.
Syntactic Preservation Theorems for Intuitionistic Predicate Logic.
Notre Dame Journal of Formal Logic,
Vol. 51,
Issue. 2,
Moniri, Morteza
2010.
Provably recursive functions of constructive and relatively constructive theories.
Archive for Mathematical Logic,
Vol. 49,
Issue. 3,
p.
291.
Arai, Toshiyasu
2011.
Quick cut-elimination for strictly positive cuts.
Annals of Pure and Applied Logic,
Vol. 162,
Issue. 10,
p.
807.
Wainer, S. S.
2017.
Logic Colloquium '01.
p.
468.
Burr, Wolfgang
2017.
Logic Colloquium '99.
p.
51.
Mojtahedi, Mojtaba
2019.
Localizing finite-depth Kripke models.
Logic Journal of the IGPL,
Vol. 27,
Issue. 3,
p.
239.
Brock‐Nannestad, Taus
and
Ilik, Danko
2019.
An intuitionistic formula hierarchy based on high‐school identities.
Mathematical Logic Quarterly,
Vol. 65,
Issue. 1,
p.
57.
Ferreira, Fernando
2020.
The FAN principle and weak König's lemma in herbrandized second-order arithmetic.
Annals of Pure and Applied Logic,
Vol. 171,
Issue. 9,
p.
102843.
Pianigiani, Duccio
and
Sorbi, Andrea
2021.
A note on uniform density in weak arithmetical theories.
Archive for Mathematical Logic,
Vol. 60,
Issue. 1-2,
p.
211.
NEMOTO, TAKAKO
and
KENTARO, SATO
2022.
A MARRIAGE OF BROUWER’S INTUITIONISM AND HILBERT’S FINITISM I: ARITHMETIC.
The Journal of Symbolic Logic,
Vol. 87,
Issue. 2,
p.
437.
Fujiwara, Makoto
and
Kurahashi, Taishi
2022.
Refining the arithmetical hierarchy of classical principles.
Mathematical Logic Quarterly,
Vol. 68,
Issue. 3,
p.
318.
Granberg Olsson, Mattias
and
Leigh, Graham E.
2024.
Revisiting the conservativity of fixpoints over intuitionistic arithmetic.
Archive for Mathematical Logic,
Vol. 63,
Issue. 1-2,
p.
61.
Fujiwara, Makoto
and
Kurahashi, Taishi
2024.
Prenex normalization and the hierarchical classification of formulas.
Archive for Mathematical Logic,
Vol. 63,
Issue. 3-4,
p.
391.
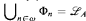
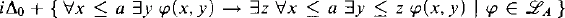 are polynomially bounded. Furthermore we show that the contrapositive of the collection-schema gives rise to instances of the law of excluded middle and hence
are polynomially bounded. Furthermore we show that the contrapositive of the collection-schema gives rise to instances of the law of excluded middle and hence 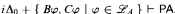 .
.