We denote by 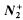and 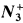the classes of torsion-free nilpotent groups of nilpotency class at most two and three, respectively. In this paper we show that most of the known results about existentially closed (e.c.) groups in 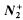remain true in 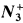: Up to isomorphism, there exist only countably many countable e.c. groups and they are distinguished by the ranks of their centers. An e.c. group is finitely (infinitely) generic if and only if the center has dimension one (≥ω). Apart from trivial exceptions, e.c, algebraically closed, and “closed with respect to systems of equations in one unknown” are equivalent.

Let K be a class of groups. A group G ϵ K is called existentially closed in K if G contains a solution of any finite system Σ of equations and inequations with constants in G and one or more unknowns, provided that Σ has a solution in some 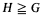in K. If Σ may contain equations (in at most n unknowns) only, G is called algebraically closed (n-unknown closed [1]). We use the abbreviations e.c, a.c and n-u.c. throughout. For more background on these terms the reader is referred to [3] and [4]. We also assume a basic knowledge of generic structures. The main group theoretic notions needed here are explained in §2; [2] and [11] are the general references for this field.