Article contents
Existence of some sparse sets of nonstandard natural numbers
Published online by Cambridge University Press: 12 March 2014
Abstract
Answers are given to two questions concerning the existence of some sparse subsets of ℋ = {0, 1 … ., H – 1} ⊆ *ℕ. where H is a hyperfinite integer. In §1. we answer a question of Kanovei by showing that for a given cut U in ℋ, there exists a countably determined set X ⊆ ℋ which contains exactly one element in each U-monad, if and only if U = a · ℕ for some a Є ℋ ∖ {0}. In §2, we deal with a question of Keisler and Leth in [6]. We show that there is a cut V ⊆ ℋ such that for any cut U, (i) there exists a U-discrete set X ⊆ ℋ with X + X = ℋ (mod H) provided 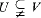 , (ii) there does not exist any U-discrete set X ⊆ ℋ with X + X = ℋ (mod H) provided
, (ii) there does not exist any U-discrete set X ⊆ ℋ with X + X = ℋ (mod H) provided 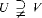 . We obtain some partial results for the case U = V.
. We obtain some partial results for the case U = V.
Information
- Type
- Research Article
- Information
- Copyright
- Copyright © Association for Symbolic Logic 2001
References
REFERENCES
- 2
- Cited by

