No CrossRef data available.
Article contents
Erdős-Rado without choice
Published online by Cambridge University Press: 12 March 2014
Abstract
A version of the Erdős-Rado theorem on partitions of the unordered n-tuples from uncountable sets is proved, without using the axiom of choice. The case with exponent 1 is just the Sierpinski-Hartogs' result that 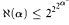 .
.
Information
- Type
- Research Article
- Information
- Copyright
- Copyright © Association for Symbolic Logic 2007
References
[1] Erdős, P., Some set-theoretical properties of graphs. Revista Universidad Nacional de Tucuman, Serie A, vol. 3 (1942), pp. 363–367.Google Scholar
[2] Erdős, P. and Rado, R., A partition calculus in set theory, The Bulletin of the American Mathematical Society, (1956), pp. 427–498.Google Scholar

