No CrossRef data available.
Article contents
THE EMBEDDING PROPERTY FOR SORTED PROFINITE GROUPS
Published online by Cambridge University Press: 20 March 2023
Abstract
We study the embedding property in the category of sorted profinite groups. We introduce a notion of the sorted embedding property (SEP), analogous to the embedding property for profinite groups. We show that any sorted profinite group has a universal SEP-cover. Our proof gives an alternative proof for the existence of a universal embedding cover of a profinite group. Also our proof works for any full subcategory of the sorted profinite groups, which is closed under taking finite quotients, fibre products, and inverse limits. We also show that any sorted profinite group having SEP has a sorted complete system whose theory is  $\omega $-categorical and
$\omega $-categorical and 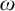 $\omega $-stable under the assumption that the set of sorts is countable.
$\omega $-stable under the assumption that the set of sorts is countable.
Keywords
MSC classification
Information
- Type
- Article
- Information
- Copyright
- © The Author(s), 2023. Published by Cambridge University Press on behalf of The Association for Symbolic Logic


