No CrossRef data available.
Article contents
The elimination of contextually defined predicates in a modal system
Published online by Cambridge University Press: 12 March 2014
Extract
In a recent note Bergmann states that “nonextensional languages may contain sentences from which contextually denned predicates are not eliminable.” A restatement of his argument is as follows. Suppose L is a functional calculus of fourth order. Included among the definitions occurring in L is
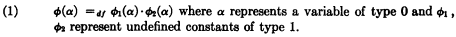
Let ϕ occur in A (where A represents a well-formed formula of L) without an argument. The elimination of ϕ from A in accordance with (1) requires

The proof of (2) depends on the principle of extensionality
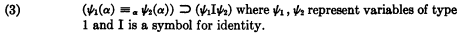
Hence Bergmann's conclusion “no such general elimination rule can be constructed for nonextensional languages.”
Information
- Type
- Research Article
- Information
- Copyright
- Copyright © Association for Symbolic Logic 1950
References
1 This Journal, vol. 13 (1948), p. 140.
2 This Journal, vol. 11 (1946), pp. 1–16 and vol. 12 (1947), pp. 12–15.

