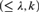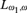Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by Crossref.
Vasey, Sebastien
2017.
Shelah's eventual categoricity conjecture in universal classes: Part I.
Annals of Pure and Applied Logic,
Vol. 168,
Issue. 9,
p.
1609.
Kruckman, Alex
2019.
Disjoint n-Amalgamation and Pseudofinite Countably Categorical Theories.
Notre Dame Journal of Formal Logic,
Vol. 60,
Issue. 1,
Baldwin, John
and
Souldatos, Ioannis
2019.
Complete Lω1,ω‐sentences with maximal models in multiple cardinalities.
Mathematical Logic Quarterly,
Vol. 65,
Issue. 4,
p.
444.
Ackerman, Nathanael
Boney, Will
and
Vasey, Sebastien
2019.
Categoricity in multiuniversal classes.
Annals of Pure and Applied Logic,
Vol. 170,
Issue. 11,
p.
102712.
Bergfalk, Jeffrey
2021.
The first omega alephs: From simplices to trees of trees to higher walks.
Advances in Mathematics,
Vol. 393,
Issue. ,
p.
108083.
Panagiotopoulos, Aristotelis
and
Shani, Assaf
2024.
Strong ergodicity phenomena for Bernoulli shifts of bounded algebraic dimension.
Annals of Pure and Applied Logic,
Vol. 175,
Issue. 5,
p.
103412.
MAZARI-ARMIDA, MARCOS
and
YANG, WENTAO
2024.
BUILDING MODELS IN SMALL CARDINALS IN LOCAL ABSTRACT ELEMENTARY CLASSES.
The Journal of Symbolic Logic,
p.
1.