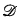 -maximal sets
-maximal setsPublished online by Cambridge University Press: 12 March 2014
In analogy to the definition of the halting problem K, an r.e. set A is called a diagonal iff there is a computable numbering ψ of the class of all partial recursive functions such that A = {i ∈ ω: ψi(i)↓} (in that case we say that A is the diagonal of ψ). This notion has been introduced in [10]. It captures all r.e. sets that can be constructed by diagonalization.
It was shown that any nonrecursive r.e. T-degree contains a diagonal, that for any diagonal A there is an r.e. nonrecursive nondiagonal B ≤TA, and that there are r.e. degrees a such that any r.e. set from a is a diagonal.
In §2 of the present paper we show that the property “A is a diagonal” is elementary lattice theoretic (e.l.t.). This result complements and generalizes previous results of Harrington and Lachlan, respectively. Harrington (see [16, XV. 1]) proved that the property of being the diagonal of some Gödelnumbering (i.e., of being creative) is e.l.t., and Lachlan [12] proved that the property of being a simple diagonal (i.e., of being simple and not hh-simple [10]) is e.l.t.
In §§3 and 4 we study the position of diagonals and nondiagonals inside the lattice of r.e. sets. We concentrate on an important class of nondiagonals, generalizing the maximal and hemimaximal sets: the 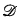 -maximal sets. Using the results from [6] we are able to classify the
-maximal sets. Using the results from [6] we are able to classify the 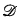 -maximal sets that can be obtained as halfs of splittings of hh-simple sets.
-maximal sets that can be obtained as halfs of splittings of hh-simple sets.