No CrossRef data available.
Article contents
Determinateness of certain almost-Borel games
Published online by Cambridge University Press: 12 March 2014
Abstract
We prove (in ZFC Set Theory) that all infinite games whose winning sets are of the following forms are determined:
(1) (A − S) ∪ B, where A is 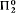 ,
, 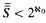 , and the game whose winning set is B is “strongly determined” (meaning that all of its subgames are determined).
, and the game whose winning set is B is “strongly determined” (meaning that all of its subgames are determined).
(2) A Boolean combination of 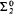 sets and sets smaller than the continuum.
sets and sets smaller than the continuum.
This also enables us to show that strong determinateness is not preserved under complementation, improving a result of Morton Davis which required the continuum hypothesis to prove this fact.
Various open questions related to the above results are discussed. Our main conjecture is that (2) above remains true when 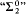 is replaced by “Borel”.
is replaced by “Borel”.
Information
- Type
- Research Article
- Information
- Copyright
- Copyright © Association for Symbolic Logic 1985
References
REFERENCES
[1]Davis, M., Infinite games with perfect information, Advances in games theory, Annals of Mathematics Studies, no. 52, Princeton University Press, Princeton, New Jersey, 1964, pp. 85–101.Google Scholar
[2]Fenstad, J. E., The axiom of determinateness, Logic Colloquium '69 (Gandy, R. O. and Yates, C. P., editors), North-Holland, Amsterdam, 1971, pp. 41–61.Google Scholar
[3]Gale, D. and Stewart, F. M., Infinite games with perfect information, Contributions to the Theory of Garnet, Annals of Mathematics Studies, no. 28, Princeton University Press, Princeton, New Jersey, 1953, pp. 245–266.Google Scholar
[4]Kuratowski, C., Topology. Vol. II, 4th ed., PWN, Warsaw, and Academic Press, New York, 1968.Google Scholar
[5]Martin, D. A., Borel determinacy, Annals of Mathematics, ser. 2, vol. 102 (1975), pp. 363–372.CrossRefGoogle Scholar
[6]Mycielski, J., On the axiom of determinateness, Fundament a Mathematkae, vol. 53 (1964), pp. 205–224.CrossRefGoogle Scholar

