Published online by Cambridge University Press: 12 March 2014
Levin and Schnorr (independently) introduced the monotone complexity, Km (α), of a binary string α. We use monotone complexity to define the relative complexity (or relative randomness) of reals. We define a partial ordering ≤Km on 2ω by α ≤Km β iff there is a constant c such that Km(α | n) ≤ Km(β | n)+ c for all n. The monotone degree of α is the set of all β such that α Km β and β Km α. We show the monotone degrees contain an antichain of size 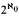 , a countable dense linear ordering (of degrees of cardinality
, a countable dense linear ordering (of degrees of cardinality 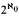 ), and a minimal pair.
), and a minimal pair.
Downey, Hirschfeldt, LaForte, Nies and others have studied a similar structure, the K-degrees, where K is the prefix-free Kolmogorov complexity. A minimal pair of K-degrees was constructed by Csima and Montalban. Of particular interest are the noncomputable trivial reals, first constructed by Solovay. We defineareal to be (Km,K)-trivial if for some constant c, Km(α | n) ≤ K(n) + c for all n. It is not known whether there is a Km-minimal real, but we show that any such real must be (Km,K)-trivial.
Finally, we consider the monotone degrees of the computably enumerable (c.e.) and strongly computably enumerable (s.c.e.) reals. We show there is no minimal c.e. monotone degree and that Solovay reducibility does not imply monotone reducibility on the c.e. reals. We also show the s.c.e. monotone degrees contain an infinite antichain and a countable dense linear ordering.