Article contents
Degree theoretic definitions of the low2 recursively enumerable sets
Published online by Cambridge University Press: 12 March 2014
Extract
The primary relation studied in recursion theory is that of relative complexity: A set or function A (of natural numbers) is reducible to one B if, given access to information about B, we can compute A. The primary reducibility is that of Turing, A ≤TB, where arbitrary (Turing) machines, φe, can be used; access to information about (the oracle) B is unlimited and the lengths of computations are potentially unbounded. Many other interesting reducibilities result from restricitng one or more of these facets of the procedure. Thus, for example, the strongest notion considered is one-one reducibility on sets: A ≤1B iff there is a one-one recursive (= effective) function f such that x Є A ⇔ f(x) Є B. Many-one (≤m) reducibility simply allows f to be many-one. Other intermediate reducibilities include truth-table (≤tt) and weak truth-table (≤wtt). The latter imposes a recursive bound f(x) on the information about B that can be used to compute A(x). The former also bounds the length of computations by requiring that the computation of A(x) from B halt in at most f(x) many steps.
Each such reducibility r defines a notion of degree, degr(A) = {B : A ≤rB ∧ B ≤rA}, and a corresponding structure 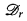 of the r-degrees ordered by r-reducibility. (We typically denote the degree of A by a.) A major theme in recursion theory has been the investigation of the relation between a set's place in these orderings (the algebraic properties of its degree) and other algorithmic, set-theoretic or definability type notions of complexity. Important examples of such other notions include rates of growth of functions, the types of approximation procedures which converge to the given function or set and the (syntactic) complexity of defining the set (or function) in arithmetic or analysis.
of the r-degrees ordered by r-reducibility. (We typically denote the degree of A by a.) A major theme in recursion theory has been the investigation of the relation between a set's place in these orderings (the algebraic properties of its degree) and other algorithmic, set-theoretic or definability type notions of complexity. Important examples of such other notions include rates of growth of functions, the types of approximation procedures which converge to the given function or set and the (syntactic) complexity of defining the set (or function) in arithmetic or analysis.
Information
- Type
- Research Article
- Information
- Copyright
- Copyright © Association for Symbolic Logic 1995
References
REFERENCES
- 11
- Cited by

