Article contents
Definability and undefinability with real order at the background
Published online by Cambridge University Press: 12 March 2014
Extract
We consider the monadic second-order theory of linear order. For the sake of brevity, linearly ordered sets will be called chains.
Let 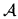 = ⟨A <⟩ be a chain. A formula ø(t) with one free individual variable t defines a point-set on A which contains the points of A that satisfy ø(t). As usually we identify a subset of A with its characteristic predicate and we will say that such a formula defines a predicate on A.
= ⟨A <⟩ be a chain. A formula ø(t) with one free individual variable t defines a point-set on A which contains the points of A that satisfy ø(t). As usually we identify a subset of A with its characteristic predicate and we will say that such a formula defines a predicate on A.
A formula 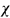 (X) one free monadic predicate variable defines the set of predicates (or family of point-sets) on A that satisfy
(X) one free monadic predicate variable defines the set of predicates (or family of point-sets) on A that satisfy 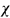 (X). This family is said to be definable by
(X). This family is said to be definable by 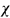 (X) in A. Suppose that
(X) in A. Suppose that 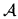 is a subchain of
is a subchain of  = ⟨B, <⟩. With a formula
= ⟨B, <⟩. With a formula 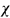 (X, A) we associate the following family of point-sets (or set of predicates) {P : P ⊆ A and
(X, A) we associate the following family of point-sets (or set of predicates) {P : P ⊆ A and 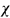 (P, A) holds in
(P, A) holds in  } on A. This family is said to be definable by
} on A. This family is said to be definable by 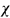 in
in 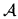 with
with  at the background.
at the background.
Note that in such a definition bound individual (respectively predicate) variables of 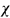 range over B (respectively over subsets of B). Hence, it is reasonable to expect that the presence of a background chain
range over B (respectively over subsets of B). Hence, it is reasonable to expect that the presence of a background chain  allows one to define point sets (or families of point-sets) on A which are not definable inside
allows one to define point sets (or families of point-sets) on A which are not definable inside 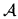 .
.
Information
- Type
- Research Article
- Information
- Copyright
- Copyright © Association for Symbolic Logic 2000
References
REFERENCES
- 5
- Cited by

