Published online by Cambridge University Press: 12 March 2014
In this paper a general method of proving the undecidability of a property P, for finite sets Σ of equations of a countable algebraic language, is presented. The method is subsequently applied to establish the undecidability of the following properties, in almost all nontrivial such languages:
1. The first-order theory generated by the infinite models of Σ is complete.
2. The first-order theory generated by the infinite models of Σ is model-complete.
3. Σ has the joint-embedding property.
4. The first-order theory generated by the models of Σ with more than one element has the joint-embedding property.
5. The first-order theory generated by the infinite models of Σ has the joint-embedding property.
A countable algebraic language ℒ is a first-order language with equality, with countably many nonlogical symbols but without relation symbols, ℒ is trivial if it has at most one operation symbol, and this is of rank one. Otherwise, ℒ is nontrivial. An ℒ-equation is a sentence of the form 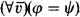 , where φ and ψ are ℒ-terms. The set of ℒ-equations is denoted by Eqℒ. A set of sentences is said to have the joint-embedding property if any two models of it are embeddable in a third model of it.
, where φ and ψ are ℒ-terms. The set of ℒ-equations is denoted by Eqℒ. A set of sentences is said to have the joint-embedding property if any two models of it are embeddable in a third model of it.
If P is a property of sets of ℒ-equations, the decision problem of P for finite sets of ℒ-equations is the problem of the existence or not of an algorithm for deciding whether, given a finite Σ ⊂ Eqℒ, Σ has P or not.