Article contents
Cylindric-relativised set algebras have strong amalgamation
Published online by Cambridge University Press: 12 March 2014
Extract
In algebra, the properties of having the (strong) amalgamation property and epis being surjective are well investigated; see the survey [10]. In algebraic logic it is shown that to these algebraic properties there correspond interesting logical properties, see e.g. [15], [12], [4], and [8, p. 311, Problem 10 and the remark below it]. In the present paper we show that the varieties Crsα (of cylindric-relativised set algebras) and Boα (of Boolean algebras with operators) have the strong amalgamation property. These contrast to the following result proved in Pigozzi [15]: No class K with Gsα ⊆ K ⊆ CAα has amalgamation property. Note that Gsα ⊆ Crsα ⊆ Boα and CAα ⊆ Boα. For related results see [3], [1], [16], [11]. For more connections with logic and abstract model theory see [14] and §4.3 of [9].
BA denotes the class of all Boolean algebras. Let α be any ordinal. From now on, throughout in the paper, α is an arbitrary but fixed ordinal. Recall from [7, p. 430, Definition 2.7.1] that an α-dimensional BA with operators, a Boα, is an algebra 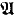 = 〈A, + −, ci, dij〉i, j ∈ α of the same similarity type as CAα's such that
= 〈A, + −, ci, dij〉i, j ∈ α of the same similarity type as CAα's such that 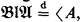 ,
, 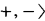 is a BA and the operations ci (i ∈ α) are additive, i.e.,
is a BA and the operations ci (i ∈ α) are additive, i.e., 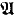 ⊨ ci(x + y) = cix + ciy for all i ⊨ α. If
⊨ ci(x + y) = cix + ciy for all i ⊨ α. If 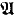 ⊨ Boα then
⊨ Boα then 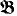 I
I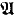 is called the Boolean reduct of
is called the Boolean reduct of 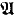 . Note that BA = Bo0. A Boα is said to be normal if {ci 0 = 0: i ∈ α} is valid in it, and a Boα is said to be extensive if {x ≤ cix: i ∈ α} is valid in it. Boα's were introduced in [17].
. Note that BA = Bo0. A Boα is said to be normal if {ci 0 = 0: i ∈ α} is valid in it, and a Boα is said to be extensive if {x ≤ cix: i ∈ α} is valid in it. Boα's were introduced in [17].
The class Crsα of all cylindric-relativised set algebras is defined in Definition 1.1.1 (iii) of [8, p. 4]. We give a definition in the present paper, too—see Definition 5 below. It is shown in [13] that ICrsα is a variety.
Our main result is (i) of Theorem 1 below, but we obtain (ii)–(vi), too, as a byproduct from the proof.
Information
- Type
- Research Article
- Information
- Copyright
- Copyright © Association for Symbolic Logic 1985
References
REFERENCES
- 20
- Cited by

