Published online by Cambridge University Press: 12 March 2014
Let L0 be a language on ℕ consisting of 0, 1, +, ∸, ·, ⌊½a⌋, ∣a∣, #, ∧(a,b), ∨(a,b), ¬(a), ≤ (a,b), and μx ≤ ∣s∣t(x). Here μx ≤ ∣s∣t(x) is the smallest number x ≤ ∣s∣ satisfying t(x) > 0 and 0 if there exist no such x and we stipulate that if s and t(a) are terms in Lo, then μx ≤ ∣s∣t(x) is also a term in Lo. The defining axioms of functions ∧(a,b), ∨(a,b), ¬(a), ≤ (a,b) are as follows:
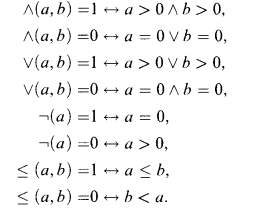
Let L a language on ℕ with only predicate constant = and L0 ⊆ L. Let f (b, a1,…,am) be a function for ℕm+1 into ℕ. We say “f is weakly expressed by terms t1(b, a1,…, am),…, tr(b, a1,…, am) in L” if for every b, a1,…, am ∈ ℕ, f (b, a1,…,am) is equal to one of ti(b, a1, …, am). The critical number of b in f with respect to L is the minimum number n such that whenever f(b, a1,…, an) is weakly expressed by terms t1(b, a1, …, an),…, the number of occurrences of b in some ti(b, a1,…, an) is at least n.
As is defined in [1], a function f is defined by a limited iteration from g and h with respect to L iff the following holds: Let τ be defined as
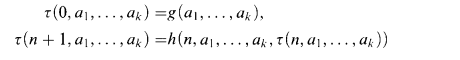
with the condition 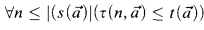 ; and
; and 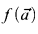 is defined by
is defined by
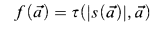
where 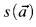 and
and 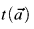 are terms in L. We say “f is defined by a short limited iteration from g and h” if
are terms in L. We say “f is defined by a short limited iteration from g and h” if 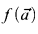 is defined by
is defined by
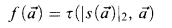
where τ, s, t are the same as above satisfying the condition 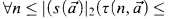
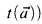 .
.