Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by Crossref.
Shami, Ziv
2006.
On analyzability in the forking topology for simple theories.
Annals of Pure and Applied Logic,
Vol. 142,
Issue. 1-3,
p.
115.
Shami, Ziv
2014.
On uncountable hypersimple unidimensional theories.
Archive for Mathematical Logic,
Vol. 53,
Issue. 1-2,
p.
203.
Shami, Ziv
2015.
A dichotomy for D-rank 1 types in simple theories.
Israel Journal of Mathematics,
Vol. 209,
Issue. 2,
p.
993.
Shami, Ziv
2016.
Continuity of SU-rank in unidimensional supersimple theories.
Archive for Mathematical Logic,
Vol. 55,
Issue. 5-6,
p.
663.

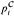 . A unidimensional simple theory eliminates the quantifier ∃
. A unidimensional simple theory eliminates the quantifier ∃