Article contents
Continuum cardinals generalized to Boolean algebras
Published online by Cambridge University Press: 12 March 2014
Extract
A number of specific cardinal numbers have been defined in terms of 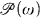 /fin or ωω. Some have been generalized to higher cardinals, and some even to arbitrary Boolean algebras. Here we study eight of these cardinals, defining their generalizations to higher cardinals, and then defining them for Boolean algebras. We then attempt to completely describe their relationships within each of several important classes of Boolean algebras.
/fin or ωω. Some have been generalized to higher cardinals, and some even to arbitrary Boolean algebras. Here we study eight of these cardinals, defining their generalizations to higher cardinals, and then defining them for Boolean algebras. We then attempt to completely describe their relationships within each of several important classes of Boolean algebras.
The generalizations to higher cardinals might involve several cardinals instead of just one as in the case of ω, For example, the number a associated with maximal almost disjoint families of infinite sets of integers can be generalized to talk about maximal subsets of [κ]μ subject to the pairwise intersections having size less than ν. (For this multiple generalization of 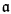 . see Monk [2001].) For brevity we do not consider such generalizations, restricting ourselves to just one cardinal. The set-theoretic generalizations then associate with each infinite cardinal κ some other cardinal λ, defined as the minimum of cardinals with a certain property.
. see Monk [2001].) For brevity we do not consider such generalizations, restricting ourselves to just one cardinal. The set-theoretic generalizations then associate with each infinite cardinal κ some other cardinal λ, defined as the minimum of cardinals with a certain property.
The generalizations to Boolean algebras assign to each Boolean algebra some cardinal λ, also defined as the minimum of cardinals with a certain property.
For the theory of the original “continuum” cardinal numbers, see Douwen [1984]. Balcar and Simon [1989]. and Vaughan [1990].
I am grateful to Mati Rubin for some conversations concerning these functions for superatomic algebras, and to Bohuslav Balcar for information concerning the function h.
The notation for set theory is standard. For Boolean algebras we follow Koppelberg [1989], but recall at the appropriate place any somewhat unusual notation.
Information
- Type
- Research Article
- Information
- Copyright
- Copyright © Association for Symbolic Logic 2001
References
REFERENCES
- 8
- Cited by

